Objektin oikeuksien ominaisuudet, yhtälöt ja esimerkit

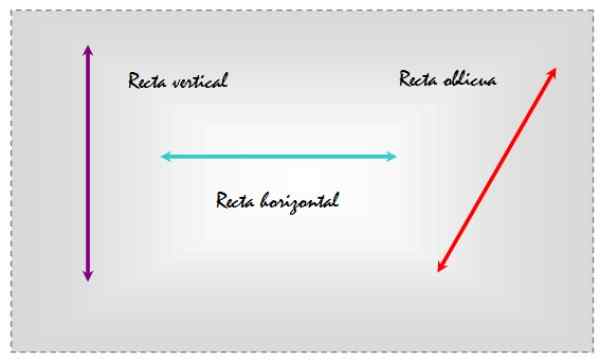
Se vino linjat Ne ovat kaltevia joko tasaisen pinnan tai muun linjan suhteen, joka osoittaa tietyn osoitteen. Esimerkiksi harkitse kolmea viivaa, jotka on piirretty seuraavaan kuvaan esiintyvään tasoon.

Tiedämme heidän vastaavat suhteelliset sijainnit, koska vertaamme heitä vertailulinjaan, joka on yleensä X -akseli Se tarkoittaa vaakasuoraa.

Kuvio 1. Pystysuorat, vaakasuorat ja vinot viivat samassa tasossa. Lähde: f. Zapata.

Tällä tavoin vaakasuuntaisen viitteen valitseminen vasen viiva on pystysuora, keskus on vaakasuora ja oikealla puolella oleva, koska se on kalteva päivittäisten referenssiviivojen suhteen.

Nyt samassa tasossa olevat viivat, kuten paperin pinta tai näytö. Ensimmäisessä tapauksessa ne ovat kuivia suorat, kun taas toisessa ne ovat yhdensuuntaisia.

Toisaalta kuivausviivat voivat olla myös vinoja tai kohtisuoria suoria linjoja. Molemmissa tapauksissa viivojen kaltevuudet ovat erilaisia, mutta vino viivat muodostuvat keskenään α- ja β -kulmat, lukuun ottamatta 90º, kun taas kohtisuoraviivat määritetyt kulmat ovat aina 90º.

Seuraavassa kuvassa nämä määritelmät on yhteenveto:

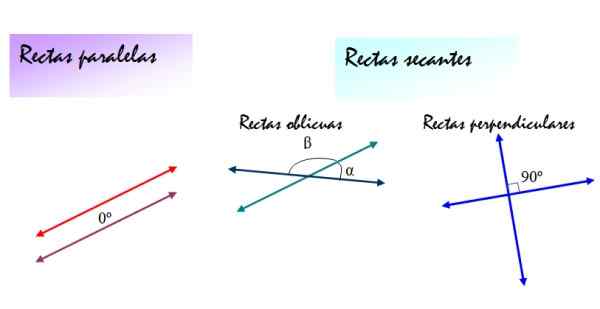Kuva 2. Suhteelliset sijainnit viivojen välillä: rinnakkaiset, vinot ja kohtisuorat eroavat toistensa kanssa muodostetussa kulmassa. Lähde: f. Zapata.

[TOC]

Yhtälöt

Tasossa olevien viivojen suhteellisten sijaintien tuntemiseksi on tarpeen tietää kulma, jonka ne muodostavat toistensa kanssa. Huomaa, että viivat ovat:

Voi palvella sinua: lähestymistapojen laskeminen erottelujen avulla

Yhdensuuntainen: Jos heillä on sama kaltevuus (yhtä suuri suunta) eivätkä koskaan leikkaa, niin heidän pisteet ovat yhtä kaukana.

Sattumaa: Kun kaikki heidän kohdat ovat samat ja siksi niillä on sama kaltevuus, mutta etäisyys niiden pisteiden välillä on nolla.

Secantes: Jos korvakorut ovat erilaisia, niiden pisteiden välinen etäisyys vaihtelee ja risteys on yksi piste.

Joten tapa tietää, ovatko kaksi koneessa olevaa viivaa kuivia vai yhdensuuntaisia, on sen kaltevuuden läpi. Viivojen rinnakkaisuuden ja kohtisuorisuuden kriteerit ovat seuraavat:

Olla kaksi riviä l₁ ja minä₂ kuuluu lentokoneeseen, jonka vireillä on vastaavasti m₁ ja m₂. Nämä viivat ovat yhdensuuntaisia, jos m₁ = m₂ ja ne ovat kohtisuorassa, kun m₁= -1/m₂

Jos tiedämme kahden viivan rinteiden rinteet, mikään edellä mainituista kriteereistä ei täyty, päättelemme, että viivat ovat vinossa. Tietäen kaksi viivan pistettä, kaltevuus lasketaan heti, kuten näemme seuraavassa osassa.

Voit selvittää, ovatko kaksi viivaa kuivia vai rinnakkain niiden risteyksen löytämistä, muodostavien yhtälöjärjestelmän ratkaisemista: Jos on liuosta, ne ovat kuivia, jos niitä ei ole yhdensuuntaisia, mutta jos liuokset ovat äärettömiä, viivat ovat sattumanvarainen.

Tämä kriteeri ei kuitenkaan ilmoita meille näiden linjojen välisestä kulmasta, vaikka niillä olisi risteys.

Linjojen välisen kulman tuntemiseksi tarvitaan kaksi vektoria tai ja v jotka kuuluvat jokaiselle. Siten on mahdollista tietää kulma, jonka ne muodostuvat vektorien skalaarituotteen läpi, määritelty tällä tavalla:

taiOllav =tai.v.cos α

Linjayhtälö tasossa

Linja Cartesian lentokoneessa voidaan edustaa monin tavoin, kuten:

Se voi palvella sinua: Yleinen Parabola -yhtälö (esimerkit ja harjoitukset)

-Virheillä tapahtuva lomake: Joo m Se on linjan kaltevuus ja b - Se on viivan leikkauspiste pystysuoran akselin kanssa, viivan yhtälö on y = mx +b.

-Yleinen yhtälö suorasta linjasta- Kirves + + c = 0, missä M = a/b Se on kaltevuus.

Cartesian -tasossa pystysuorat ja vaakasuorat viivat ovat tietyissä tapauksissa viivayhtälön.

-Pystysuora viivat- x = a

-Vaakasuora viivat- y = k

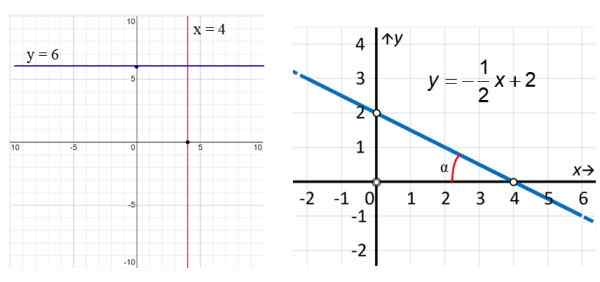Kuva 3. Vasemmalla pystysuora viiva x = 4 ja vaakaviiva y = 6. Oikealla esimerkki vinosta linjasta. Lähde: f. Zapata.

Kuvion 3 esimerkeissä pystysuoralla punaisella viivalla on yhtälö x = 4, kun taas X -akselin (sinisen) yhdensuuntaisella viivalla on yhtälö y = 6. Oikean viivan suhteen näemme, että se on vino ja löytää yhtälö, käytämme kuvassa korostettuja pisteitä: (0,2) ja (4.0) tällä tavalla:

M = (ja₂ - ja₁) / (X₂ - x₁) = (2 - 0) / (0 - 4) = - ½

Tämän viivan leikkaus pystysuoran akselin kanssa on y = 2, Kuten grafiikasta todettiin. Näiden tietojen kanssa:

y = (-½) x+2

Kaltevuuskulman määrittäminen x -akseliin on yksinkertaista. Minusta tuntuu että:

α = arctg (2/4) = 26.Kuudes

Siksi positiivinen kulma x -akselista linjaan on: 180º - 26.6. = 153.Neljäs

Esimerkkejä vinoista linjoista

Kuva 4. Esimerkkejä vinoista linjoista. Lähde: Ian Patterson Vihainen [CC by (https: // creativecommons.Org/lisenssit/by/2.0)]. Pisan kalteva torni. Pixabay.

Viblis -linjat ilmestyvät monissa paikoissa, on kiinnitettävä huomiota niiden löytämiseen arkkitehtuurista, urheilusta, sähkönjakelujen johdoista, putkista ja monissa muissa paikoissa. Luonnossa on myös vino linjoja, kuten alla näemme:

Voi palvella sinua: johdannaisäännöt (esimerkkien kanssa)

Valonsäteet

Auringonvalo leviää suorassa linjassa, mutta maan pyöristetty muoto vaikuttaa tapaan, jolla auringonvalo vaikuttaa pintaan.

Alla olevassa kuvassa voimme selvästi arvostaa, että aurinkosäteet vaikuttavat kohtisuoraan trooppisilla alueilla, mutta sen sijaan ne saapuvat vinosti maltillisten alueiden pintaan ja pylväissä.

Siksi auringonsäteet kulkevat pidemmän matkan ilmakehän läpi ja myös lämpö leviää suuremmalle pinnalle (katso kuva). Tuloksena on, että pylväiden lähellä olevat alueet ovat kylmempiä.

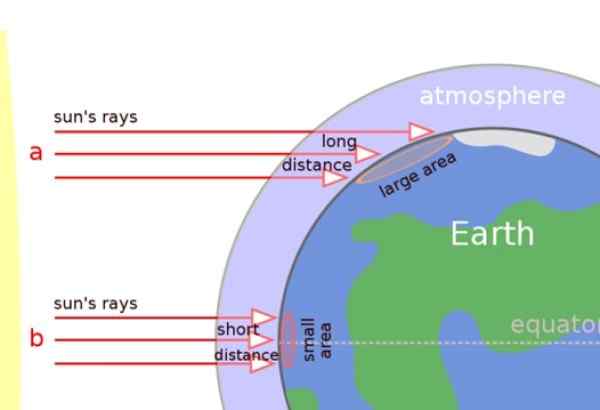Kuva 5. Auringonsäteet vaikuttavat vinosti maltillisiin vyöhykkeisiin ja napoihin, mutta ne ovat enemmän tai vähemmän kohtisuorassa tropiikissa. Lähde: Wikimedia Commons.

Linjat, jotka eivät ole samassa tasossa

Kun kaksi linjaa ei ole samassa tasossa, ne voivat silti olla vinoja tai kiitetty, kuten myös tunnetaan. Tässä tapauksessa sen ohjaajat eivät ole yhdensuuntaisia, mutta eivät kuulu samaan tasoon, näillä viivoilla ei ole risteystä.

Esimerkiksi oikean kuvan linjat ovat selvästi eri tasoilla. Jos ne katsovat ylhäältä, havaitaan, että ne ylittävät tehokkaasti, mutta heillä ei ole yhteistä pistettä. Oikealla puolella näemme polkupyöräpyörät, joiden säteet näyttävät ylittävän, kun ne näyttävät suoraan eteenpäin.

Kuva 6. Eri lentokoneille kuuluvat viivat linjat. Lähde: vasen f. Zapata, oikea pixabay.

Viitteet

1. Geometria. Linjan vektorijohtaja. Toipunut: Juanbragado.On.
2. Larson, r. 2006. Laskenta analyyttisellä geometrialla. Kahdeksas. Painos. McGraw Hill.
3. Matematiikka on peli. Linjat ja kulmat. Toipunut: Juntadeandalucia.On.
4. Linjat, jotka ylittävät. Toipunut: Teacheraltuna.com.
5. Villena, m. Analyyttinen geometria R3: ssa. Haettu osoitteesta: dspace.Espoli.Edu.EY.