Riemannin historian, kaavojen ja ominaisuuksien, harjoitusten summa

Se Riemann -summa Se on nimi, joka vastaanottaa määritellyn integraalin likimääräisen laskelman huomattavan summan avulla äärellisillä termeillä. Yleinen sovellus on funktio -alueen lähestymistapa graafisessa.

Se oli saksalainen matemaatikko Georg Friedrich Bernhard Riemann (1826-1866), joka tarjosi ensimmäistä kertaa tiukan määritelmän funktion integroinnista tietyllä aikavälillä. Hän ilmoitti siitä vuonna 1854 julkaistussa artikkelissa. 

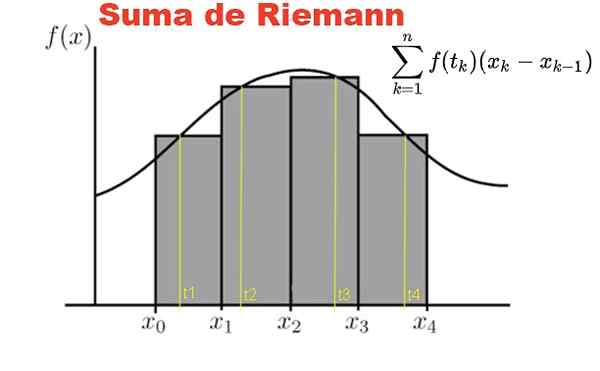
Kuvio 1. Riemannin summa määritetään F -funktiossa ja osiossa aikavälillä [x0, x1]. Lähde: Fanny Zapata.

Riemannin summa määritetään y = f (x) -funktiossa, ja X kuuluu suljetulle aikavälille [A, B]. Tällä aikavälillä tehdään N -elementtien osio P:

P = x_{0 -}= a, x₁, x₂,…, X_n= b

Tämä tarkoittaa, että aika on jaettu seuraavasti:

 Täällä t_{k -k -} on välillä x_K-1 ja x_{k -k -}-

x_K-1 ≤ t_{k -k -} ≤ x_{k -k -}

Kuvio 1 näyttää F -funktion riemannin summan aikavälillä [x_{0 -}, x₄] Neljän subintervaarin osiossa harmaat suorakulmiot.

Summa edustaa suorakulmioiden kokonaispinta -alaa ja tämän summan tulos on numeerisesti lähestymistapa käyrän F abstantin alla olevalle alueelle Abscissas X = X: n joukossa_{0 -} y x = x₄.

Tietysti lähestymistapa käyrän alla olevaan alueelle paranee huomattavasti siinä määrin kuin lukumäärä n osioista on suurempi.  Tällä tavoin summa lähentyy käyrän alla olevaan alueeseen, kun numero n osioilla on taipumus äärettömyyteen.

[TOC]

Kaavat ja ominaisuudet

Riemannin F (x) -funktion summa osiossa:

Voi palvella sinua: Rhomboid: Ominaisuudet, kuinka kehä ja alue vie pois

P = x_{0 -}= a, x₁, x₂,…, X_n= b

Määritelty aikavälillä [a, b], sen annetaan:

S (p, f) = ∑_{K = 1}ⁿ f (t_{k -k -}) (x_{k -k -} - x_K-1-A 

Missä t_{k -k -} Se on arvoa [x_{k -k -}, x_K-1-. Riemannin summassa säännöllisiä leveysvälejä käytetään yleensä Δx = (b - a)/n, missä a ja b ovat abskissan minimi- ja maksimiarvoja, kun taas n on alajakojen lukumäärä.

Siinä tapauksessa Riemannin oikea summa On:

Sd (f, n) = [f (a+Δx)+f (a+2δx)+…+f (a+(n-1) Δx)+f (b)]*Δx

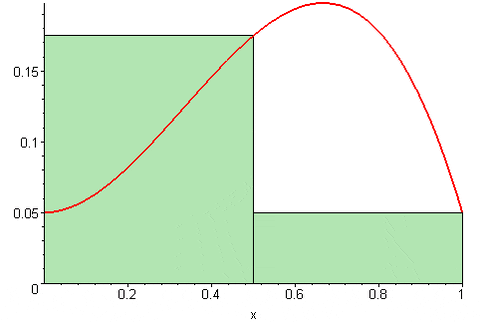Kuva 2. Riemannin oikea summa. Lähde: Wikimedia Commons. 09GLASGOW09 [CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/3.0)].

Samalla kun Riemannin vasen summa Se ilmaistaan ​​seuraavasti:

Kyllä (f, n) = [f (a)+f (a+Δx)+…+f (a+(n-1) Δx)]*Δx

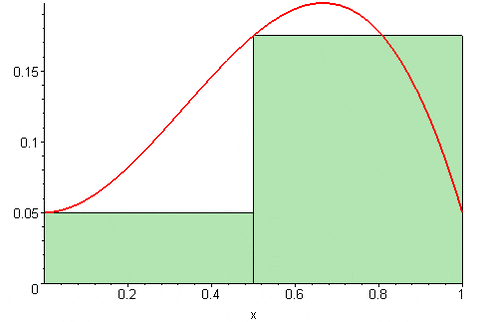Kuva 3. Riemannin summa lähti. Lähde: Wikimedia Commons. 09GLASGOW09 [CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/3.0)]

Lopuksi Riemannin keskussumma On:

Sc (f, n) = [f (a+Δx/2)+f (A+3AX/2)+…+f (b- Δx/2)]*Δx

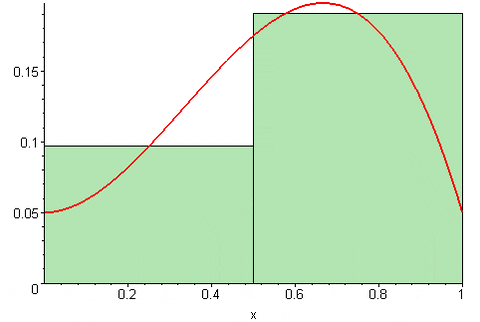Kuva 4. Riemannin välisumma. Lähde: Wikimedia Commons. 09GLASGOW09 [CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/3.0)]

Riippuen siitä, missä piste t sijaitsee_{k -k -} Välein [x_{k -k -}, x_K-1] Riemannin summa voi yliarvioida tai aliarvioida y = f (x) -funktiokäyrän alla olevan alueen tarkan arvon (x). Ts.

Käyrän alla oleva alue

Riemannin summan pääominaisuus ja josta sen tärkeys tulee, on se, että jos alajakojen lukumäärä on taipumus äärettömyyteen, summan tulos lähenee funktion määritettyyn integraalia:

Aikaisempi lauseke vastaa Riemannin kiinteän määritelmän määritelmää ja sovelletaan edellyttäen, että F -funktio on jatkuva ja pehmeä. Erityisempiä toimintoja varten on muitakin määritelmiä integraalille (Integral de stilldjes ja Integral de lebesgue).

Se voi palvella sinua: Vakio arviointivirhe: miten se lasketaan, esimerkkejä, harjoituksia

Ratkaisut

- Harjoitus 1

Laske funktion a = -2 -B = +2 välillä määritellyn integraalin arvo:

f (x) = x²

Käytä summaa Riemannia. Tätä varten etsi summa välin säännöllisistä osioista [a, b] ja ota sitten matemaattinen raja tapaukselle, että osioiden lukumäärä myydään äärettömyyteen. 

Ratkaisu

Nämä ovat seuraavat vaiheet:

-Ensinnäkin osioväli määritellään seuraavasti: 

Δx = (b - a)/n. 

-Sitten oikealla oleva Riemann -summa, joka vastaa funktiota f (x), on tällainen:

-Nyt ne korvataan a = -2 ja b =+2, niin että väli tai vaihe Δx = 4/n. Toisin sanoen Riemannin summa funktiolle f (x) = x² On:

-Sitten kehitetään neliömäinen binomi: 

[-2 +(4i/n)]² = 4 - (16 I /N) + (4 /N)² Yllyttää²

-Ja sitten se korvataan huolellisesti summana:

-Seuraava vaihe on erottaa yhteenvedot ja poistaa vakiot määrät kunkin summan yleisenä tekijänä. On tarpeen ottaa huomioon, että hakemisto on I, siten numerot ja ehdot n Niitä pidetään vakiona:

-Jokainen summa arvioidaan, koska jokaiselle niistä on asianmukaisia ​​lausekkeita. Esimerkiksi ensimmäinen yhteenvedoista:

Toinen on:

 Ja kolmas on:

 -Riemannin summan yhteenvetojen tulosten korvaaminen lopulta saadaan:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

-Viimeinkin sinun on laskettava integraali on:

= Lim_N➝∞ [16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²] =

= 16 -(64/2) + (64/3) = 16/3 = 5,333

Lukija voi varmistaa, että tämä on tarkka tulos, joka voidaan saada ratkaisemalla määrittelemätön integraali ja arvioimalla integroinnin rajat Barrow -sääntöllä.

Voi palvella sinua: Kuinka muuntaa km/h a m/s? Ratkaisut

- Harjoitus 2

Määritä suunnilleen funktion alla oleva alue: 

f (x) = (1/√ (2π) e^(-X2/2)

Välillä x = -1 ja x =+1, käyttämällä Riemannin keskussummaa 10 osiolla. Vertaa tarkkaan tulokseen ja arvioi prosentuaalinen ero.

Ratkaisu

Vaihe tai lisäys kahden peräkkäisen erillisen arvon välillä on:

Δx = (1 - (-1)/10 = 0,2

Niin että P -osa, jolla suorakulmiot on määritelty, on tällainen:

P = -1,0; -0,8; -0,6; -0.4; -0,2; 0,0; 0,2; 0,4; 0,6; 0,8; 1.0

Mutta kuten haluat, on keskeinen summa, funktio F (x) arvioidaan alaryhmien keskipisteissä, toisin sanoen sarjassa:

T = -0,9; -0,7; -0,5; -0,3; -0,1; 0,1; 0,3; 0,5; 0,7; 0,9.

Riemannin summa (keskeinen) on tällainen:

S = f (-0,9)*0,2 +f (-0,7)*0,2 +f (-0,5)*0,2 +… +f (0,7)*0,2 +f (0,9)*0,2

Koska F -funktio on symmetrinen, on mahdollista vähentää summa vain viiteen termiin ja tulos kerrotaan kahdella:

S = 2*0,2*f (0,1)+ f (0,3)+ f (0,5)+ f (0,7)+ f (0,9)

S = 2*0,2*0,397+ 0,381+ 0,352+ 0,312+ 0,266 = 0,683

Tässä esimerkissä annettu funktio ei ole kukaan muu kuin hyvin tunnettu Gauss Bell (normalisoitu, keskimäärin nolla ja keskihajonta yksi). On tiedossa, että tämän funktion käyrän alla oleva alue [-1,1] on 0,6827.

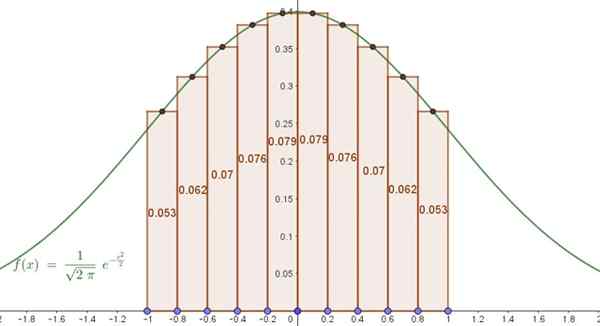Kuva 5. Alue likimääräisen Gauss Bellin alla Riemannin summan avulla. Lähde: f. Zapata.

Tämä tarkoittaa, että likimääräinen ratkaisu, jolla on vain 10 termi. Arvioidun integraalin ja tarkan välinen prosentuaalinen virhe on 0,07%.

Viitteet

1. Casteleiro, J. M., & Gómez-Alvarez, R. P. (2002). Kattava laskelma (kuvitettu ED.-A. Madrid: ESIC -toimitus.
2. Yksikaani. Integraalin käsitteen historia. Palautettu: arkistosta.Yksikaani.On
3. Uis. Riemann sumut. Toipunut: matematiikka.Uis.Edu.yhteistyö
4. Wikipedia. Riemann -summa. Palautettu: on.Wikipedia.com
5. Wikipedia. Riemannin integrointi. Palautettu: on.Wikipedia.com