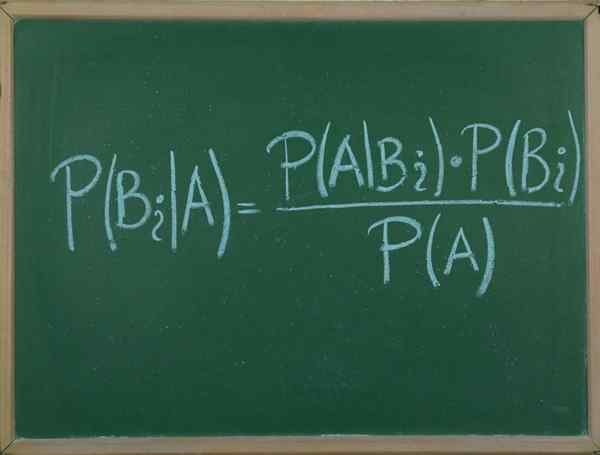Bayes -lause
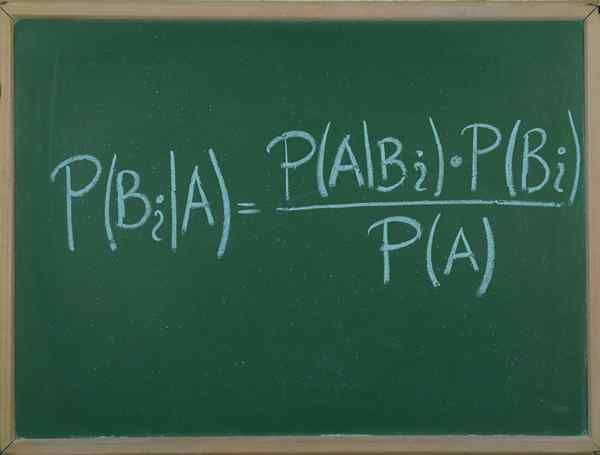
- 3829
- 542
- Juan Breitenberg V
Selitämme, mikä on Bayesin lause, sen sovellukset ja laitamme harjoitukset ratkaistu
Mikä on Bayesin lause?
Hän Bayes -lause Se on menettely, jonka avulla voimme ilmaista satunnaisen tapahtuman A ehdollisen todennäköisyyden D -noppaa B, annetun tapahtuman B jakautumisen ja vain todennäköisyyden jakautumisen suhteen.
Tämä lause on erittäin hyödyllinen, koska sen ansiosta voimme liittyä todennäköisyyden, että tapahtuma tapahtuu tietäen, että B tapahtui, todennäköisyydellä, että päinvastoin tapahtuu, ts.
Bayesin lause oli kunnioittaja Thomas Bayes, kahdeksannentoista vuosisadan englantilainen teologi, joka oli myös matemaatikko. Hän oli kirjoittanut useita teologian työpaikkoja, mutta tällä hetkellä hänet tunnetaan parista matemaattisista sopimuksista, joista Bayesin lause on jo mainittu päätulokseksi.
Bayes käsitteli tätä lausetta teoksessa, jonka otsikko on "Essee ongelman ratkaisemiseksi mahdollisuuksien opissa" (essee, joka ratkaisee ongelman mahdollisuuksien opissa), julkaistu vuonna 1763 ja jolla on suuria tutkimuksia sovellusten kanssa eri tietoalueilla.
Selitys
Ensinnäkin tämän lauseen suuremman puristamiseksi ovat välttämättömiä joitain todennäköisyysteorian peruskäsityksiä, etenkin kuntolause ehdollisen todennäköisyyden kannalta, mikä osoittaa sen
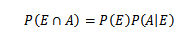
E: lle ja mielivaltaisille tapahtumille näytetilasta S.
Ja osioiden määritelmä, joka kertoo meille, että meillä on1 ,-Lla2,…,n Näytetilan tapahtumat, nämä muodostavat S: n, jos aYllyttää Ne ovat toisiaan poissulkevia ja heidän liitto on.
Voi palvella sinua: mitkä ovat numerot? 8 pääkäyttöäTällä on toinen tapahtuma. Joten voimme nähdä b: n
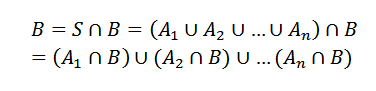
MissäYllyttää B: n kanssa leikkaus ovat toisiaan poissulkevia tapahtumia.
Ja sen seurauksena,
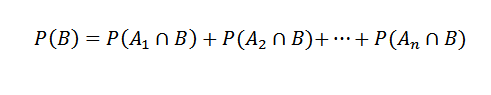
Sitten kertomalla kertolaskulause
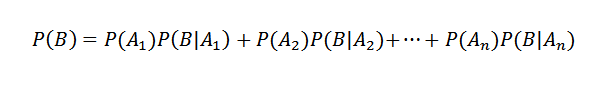
Toisaalta AI B: n ehdollinen todennäköisyys on määritelty
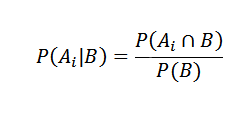
Korvataan oikein, meillä on se jokaiselle I
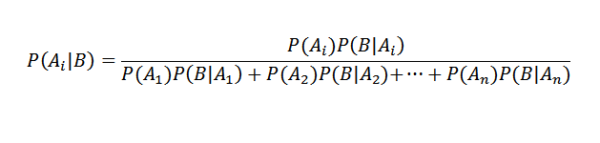
Bayes -lausekeskukset
Tämän tuloksen ansiosta tutkimusryhmät ja monipuoliset yritykset ovat onnistuneet parantamaan tietoon perustuvia järjestelmiä.
Tautitutkimus
Esimerkiksi sairauksien tutkimuksessa Bayesin lause voi auttaa havaitsemaan todennäköisyyden, että sairaus löytyy ihmisistä, joilla on tietty ominaisuus, ottaen tietoon taudin globaalit määrät ja mainitun ominaisuuden hallussapito molemmissa Terveet ja sairaat ihmiset.
Ohjelmistokehitys
Toisaalta korkean tekniikan maailmassa se on vaikuttanut suuriin yrityksiin, jotka ovat kehittäneet tämän tuloksen ansiosta, ohjelmisto "tietoon perustuvat".
Päivittäisenä esimerkkinä meillä on Microsoft Office Assistant. Bayesin lause auttaa ohjelmistoja arvioimaan käyttäjän esittämiä ongelmia ja määrittämään, mitä neuvoja tarjotaan ja pystyy siten tarjoamaan parempaa palvelua käyttäjän tottumusten mukaisesti.
On huomattava, että tätä kaavaa jätettiin huomiotta viime aikoina, tämä johtuu pääasiassa siitä, että kun tämä tulos kehitettiin 200 vuotta sitten, heille ei ollut juurikaan käytännöllistä käyttöä. Aikana, suuren teknologisen kehityksen ansiosta tutkijat ovat kuitenkin saavuttaneet tapoja toteuttaa tämä tulos käytännössä.
Ratkaisut
Harjoitus 1
Matkapuhelinyhtiöllä on kaksi A- ja B -konetta. 54% matkapuhelimista on valmistettu koneella A ja loput koneella B. Kaikki matkapuhelimet eivät ole hyvässä kunnossa.
Voi palvella sinua: tekijäA: n tekemien viallisten matkapuhelimien osuus on 0.2 ja B: lle on 0.5. Mikä on todennäköisyys, että mainitun tehtaan matkapuhelin on viallinen? Mikä on todennäköisyys, että tietäen, että matkapuhelin on viallinen, tulee koneesta?
Ratkaisu
Täällä sinulla on kokeilu, joka suoritetaan kahdessa osassa; Ensimmäisessä osassa tapahtumia esiintyy:
TO: Machine A: n valmistama matkapuhelin.
B: Machine B: n valmistama matkapuhelin.
Koska kone A tuottaa 54% matkapuhelimista ja loput tuotetaan koneella B, koneen B on tuotettava 46% matkapuhelimista. Näiden tapahtumien mahdollisuudet annetaan, nimittäin:
P (a) = 0,54.
P (b) = 0,46.
Kokeen toisen osan tapahtumat ovat:
D: Viallinen matkapuhelin.
E: Ei -tyydyttämätön solu.
Kuten lausunnossa todetaan, näiden tapahtumien todennäköisyydet riippuvat ensimmäisessä osassa saadusta tuloksesta:
P (d | a) = 0,2.
P (d | b) = 0,5.
Näiden arvojen avulla voit myös määrittää näiden tapahtumien lisävarusteiden todennäköisyydet, ts
P (e | a) = 1 - p (d | a)
= 1 - 0,2
= 0,8
ja
P (e | b) = 1 - p (d | b)
= 1 - 0,5
= 0,5.
Nyt D -tapahtuma voidaan kirjoittaa seuraavasti:
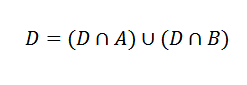 Nämä tapahtumat ovat toisiaan poissulkevia.
Nämä tapahtumat ovat toisiaan poissulkevia.
Kertolaskelman käyttäminen ehdolliselle todennäköisyydelle on:
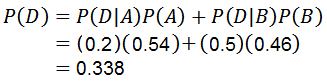
Jonka kanssa ensimmäiseen kysymykseen vastataan.
Nyt meidän on vain laskettava P (A | D), jolle Bayesin lause sovelletaan:
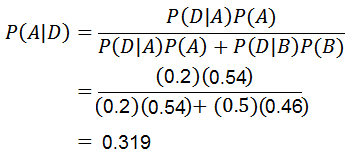
Bayesin lauseen ansiosta voidaan vahvistaa, että koneen A.319.
Voi palvella sinua: IcosagonoHarjoitus 2
Kolme laatikkoa sisältää mustia ja mustia palloja. Kunkin niistä koostumus on seuraava: u1 = 3b, 1n, u2 = 2b, 2n, u3 = 1b, 3n.
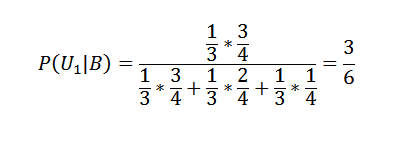
Satunnaisesti valittu yksi laatikoista ja satunnainen pallo uutetaan siitä, mikä osoittautuu valkoiseksi. Mikä on laatikko, jonka todennäköisimmin on valittu?
Ratkaisu
U1: n, U2: n ja U3: n kautta edustamme myös valittua laatikkoa.
Nämä tapahtumat muodostavat S -osion ja varmistetaan, että p (u1) = p (u2) = p (u3) = 1/3, koska laatikon valinta on satunnainen.
Jos b = uutettu pallo on valkoinen, meillä on p (b | u1) = 3/4, p (b | u2) = 2/4, p (b | u3) = 1/4 .
Mitä haluamme saada, on todennäköisyys, että pallo on otettu IU -laatikosta tietäen, että tämä pallo oli valkoinen, ts. P (ui | b), ja nähdä, mitkä kolmesta arvosta oli korkein tietää mikä joista laatikko on todennäköisemmin poiminut valkoisen pallon.
Bayesin lauseen soveltaminen ensimmäiseen laatikoihin:
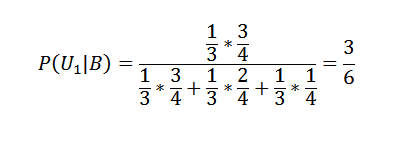
Ja kahdelle muulle:
P (u2 | b) = 2/6 ja p (u3 | b) = 1/6.
Sitten ensimmäinen laatikoista on se, jolla on suurempi todennäköisyys, että se on valittu valkoisen pallon uuttamiseen.