Lämmönsiirtolakit, lähetysmuodot, esimerkit

Olemassa lämmönsiirto Kun energia siirtyy kehosta toiseen, koska lämpötilaerot ovat näiden kahden välillä. Lämmönsiirtoprosessi lakkaa heti, kun kosketuksessa olevien runkojen lämpötilat tasoitetaan tai kun niiden välinen kosketus on tukahdutettu.

Tietyn ajanjakson aikana kehosta toiseen siirretyn energian määrää kutsutaan Lämmön siirretty. Yksi runko voi antaa lämmön toiselle tai se voi absorboida sen, mutta lämpö siirtyy aina korkeimmasta lämpötilan rungosta alimpaan lämpötilaan.

Kuvio 1. Kokoonpanossa annetaan kolme lämmönsiirtomekanismia: ajaminen, konvektio ja säteily. Lähde: Pixabay.

Lämpöyksiköt ovat samat kuin energian ja kansainvälisen mittausjärjestelmän (SI). Muita usein käytettyjä lämpöyksiköitä ovat kalori ja BTU. 

Lämmönsiirtoa hallitsevien matemaattisten lakien osalta nämä riippuvat vaihtoon puuttuvasta mekanismista. 

Kun lämpöä suoritetaan rungosta toiseen, lämmön vaihtamisen nopeus on verrannollinen lämpötilaeroon. Tämä tunnetaan nimellä Fourierin laki lämmönjohtavuutta, mikä johtaa Newtonin jäähdytyslaki.

[TOC]

Muodot/lämmönsiirtomekanismit

Ne ovat tapoja, joilla lämpö voidaan vaihtaa kahden ruumiin välillä. Kolme mekanismia tunnustetaan:

-Ajo

-Konvektio

-Säteily

Yllä olevassa kuvassa esitetyssä potissa on näitä kolme lämmönsiirtomekanismia:

-Potin metalli lämmitetään pääasiassa ajamalla.

-Vettä ja ilmaa lämpöä ja nouse konvektiolla.

-Potin lähellä olevat ihmiset lämmitetään säteilyllä.

Ajo

Lämmönjohtavuus tapahtuu enimmäkseen kiinteissä aineissa ja erityisesti metalleissa.

Esimerkiksi keittiön sarvi välittää lämmön ruuan ruuan sisällä metallin ajomekanismin ja astian metalliseinien läpi. Lämpöjohtavuudessa ei ole materiaalia, vain energiaa.

Konvektio

Konvektiomekanismi on tyypillinen nesteille ja kaasuille. Melkein aina nämä ovat vähemmän tiheitä korkeammassa lämpötilassa, tästä syystä lämmönkuljetus on nousevassa kuumimmassa nesteessä korkeille alueille kylmimmällä nesteellä. Konvektiomekanismissa on materiaalikuljetus. 

Voi palvella sinua: Epävakaa tasapaino: Konsepti ja esimerkit

Säteily

Säteilymekanismi puolestaan ​​sallii lämmönvaihdon kahden kappaleen välillä, vaikka ne eivät olisi kosketuksissa. Välitön esimerkki on aurinko, joka lämmittää maan tyhjän tilan läpi kahden välissä. 

Kaikki kappaleet lähettävät ja imevät sähkömagneettisen säteilyn. Jos sinulla on kaksi runkoa eri lämpötiloissa, jopa tyhjiössä, hetken kuluttua ne saavuttavat saman lämpötilan johtuen sähkömagneettisen säteilyn kalorien vaihdosta.

Kalorinsiirto

Tasapainossa olevissa termodynaamisissa järjestelmissä se tuo ympäristöä vaihdetun kokonaislämpömäärän siten, että järjestelmä kulkee tasapainosta toiseen.

Toisaalta lämmönsiirto, korko keskittyy väliaikaiseen ilmiöön, kun järjestelmät eivät ole vielä saavuttaneet lämpötasapainoa. On tärkeää huomata, että lämmön määrä vaihdetaan tietyllä ajanjaksolla, ts.

Esimerkit

- Lämmön ajo -esimerkit

Lämmönjohtavuudessa lämpöenergia siirtyy materiaalin atomien ja molekyylien välisillä törmäyksillä, olipa tämä kiinteä, neste tai kaasu. 

Kiinteät aineet ovat parempia lämmönjohtimia kuin kaasut ja nesteet. Metalleissa on vapaita elektroneja, jotka voivat liikkua metallin ympäri.

Koska ilmaisilla elektroneilla on suuri liikkuvuus, he kykenevät siirtämään kineettisen energian törmäyksellä tehokkaammin, joten metalleilla on korkea lämmönjohtavuus.

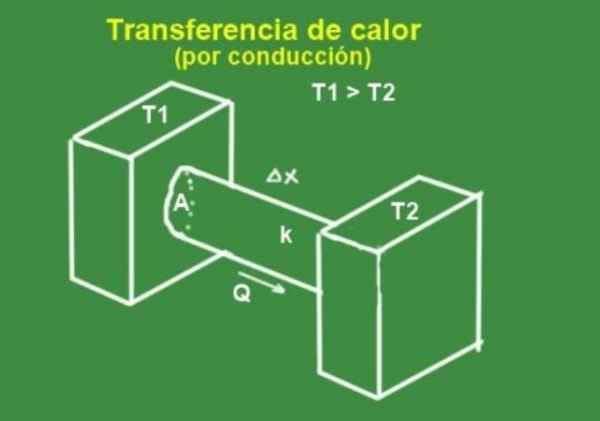
Makroskooppisesta näkökulmasta lämmönjohtavuus mitataan siirretyn lämpöyksikköä kohti tai kalorivirran H:

Kuva 2. Lämmönjohtavuus baarin kautta. Valmistettu Fanny Zapata.

Kalorivirta H on verrannollinen poikkileikkaukseen -Lla ja pitkittäisetäisyyden lämpötilan vaihtelussa.

Aikaisempi kaava tunnetaan nimellä Fourierin laki ja suhteellisuusvakio k -k - Se on lämmönjohtavuus. 

Tätä yhtälöä käytetään kalorivirran laskemiseen H baarista, kuten kuviossa 2, joka on kahden lämpötilasäiliön välillä T₁ ja T₂ vastaavasti oleminen T₁T₂.

Materiaalien lämmönjohtavuus

Alla on luettelo joidenkin Watt -materiaalien lämmönjohtavuudesta Kelvinissä: w/(M . K) 

Voi palvella sinua: Galileo Galilei ja hänen vapaa syksyn laki

Alumiini -205

Kupari -385

Hopea --400

Teräs -50

Korkki tai lasikuitu- 0,04

Betoni tai lasi -0.8

Puu- 0,05- 0,015

Ilma - 0,024

- Lämpöesimerkkejä konvektiolla

Lämpökonvektiossa energia siirretään nesteen liikkumisen vuoksi, jolla eri lämpötiloissa on erilaiset tiheydet. Esimerkiksi, kun kiehuvaa vettä ruukkuun, vesi lähellä pohjaa nostaa lämpötilaa, joten se laajenee.

Tämä laajentuminen aiheuttaa kuuman veden nousun, kun taas kylmä matala miehittää kiipeilyn kuuman veden jättämää tilaa. Tuloksena on kiertoliike, joka jatkuu, kunnes kaikkien tasojen lämpötilat ovat yhtä suuret.

Konvektio on se, joka määrittelee maapallon ilmakehän suurten ilmamassojen liikkumisen ja määrittää myös merivirtojen kiertämisen.

- Lämpöesimerkkejä säteilyllä

Lämmönsiirron mekanismeissa johtavuuden ja konvektion avulla materiaalin läsnäolo vaaditaan siten, että lämpö välitetään. Toisaalta säteilymekanismissa lämpö voi kulkea ruumiista toiseen tyhjyyden läpi.

Tämä on mekanismi, jolla aurinko, korkeammassa lämpötilassa kuin maa, välittää energiaa planeetallemme suoraan tilan tyhjyyden avulla. Säteily saavuttaa meidät sähkömagneettisilla aaltoilla.

Kaikki materiaalit kykenevät säteilemään ja absorboimaan sähkömagneettista säteilyä. Lähetetty tai absorboitu suurin taajuus riippuu materiaalin lämpötilasta ja mainittu taajuus kasvaa lämpötilan kanssa.

Mustan rungon päästö- tai absorptiospektrin hallitseva aallonpituus seuraa Laki, joka osoittaa, että vallitseva aallonpituus on verrannollinen kehon lämpötilan käänteiseen.

Toisaalta teho (wattissa), jolla runko emittoi tai absorboi kalorienergiaa sähkömagneettisen säteilyn avulla. Tämä tunnetaan nimellä Stefanin laki-

P = εaσt⁴

Edellisessä ilmaisussa σ Se on Stefanin vakio ja sen arvo on 5,67 x 10-8 W/m² K -k -⁴. -Lla Se on kehon pinnan alue ja ε Se on materiaalin säteily, vakio ilman mittoja, joiden arvo on välillä 0 ja 1, ja riippuu materiaalista.

Voi palvella sinua: isobarinen prosessi: kaavat, yhtälöt, kokeet, harjoitukset

Liikuntaa

Harkitse kuvassa 2. Oletetaan, että palkki on 5 cm pitkä, 1 cm säde ja se on kuparia.

Baari on asetettu kahden seinän väliin, jotka ylläpitävät sen vakio lämpötilaa. Ensimmäisessä seinämässä on lämpötila T1 = 100ºC, kun taas toinen on t2 = 20ºC. Päättää:

-lla.- Lämpövirran H arvo

b -.- Kuparipalkin lämpötila 2 cm, 3 cm ja 4 cm lämpötilaseinästä T1.

Liittää jhk

Koska kuparin palkki on sijoitettu kahden seinän väliin, joiden seinät ylläpitävät samaa lämpötilaa aina, voidaan sanoa, että se on paikallaan olevassa järjestelmässä. Toisin sanoen lämpövirralla H: llä on sama arvo milloin tahansa.

Tämän virran laskemiseksi käytämme kaavaa, joka yhdistää virran H: n lämpötilaeroon ja palkin pituuteen.

Koska palkki on kuparia, tiedämme aiemmin osoitetussa taulukossa, että sen lämmönjohtavuus K -toski: 385 w/(m k).

Poikkileikkaus on:

A = πr² = 3,14*(1 × 10^-2m)² = 3,14 x 10^-4 m²

Lämpötilaero palkin päiden välillä on

Δt = (100ºC - 20ºC) = (373k - 293k) = 80k

Δx = 5 cm = 5 x 10^-2 m

H = 385 w/(m k) * 3,14 x 10^-4 m² * (80k /5 x 10^-2 m) = 193,4 W

Tämä virta on sama missä tahansa baarissa ja milloin tahansa, koska paikallaan oleva järjestelmä on saavutettu.

Ratkaisu b

Tässä osassa meitä pyydetään laskemaan lämpötila TP kohdassa P etäisyyden päässä XP Suhteessa seinään T₁.

Ilmaisu, joka antaa kalorivirran H asiaan P On:

H = k a (t₁ -Tp)/(xp)

Tästä lausekkeesta se voidaan laskea TP kautta:

Tp = t₁ - (H XP) / (K A) = 373 K - (193,4 W / (385 W / (M K) 3,14 x 10^-4 m²))*XP

TP = 373 K - 1620,4 (K/M) * XP

Lasketaan lämpötila TP Asennoissa 2 cm, 3 cm ja 4 cm korvaamalla numeeriset arvot:

• TP = 340,6K = 67,6 ºC; 2 cm: n päässä T1
• TP = 324,4K = 51,4 ºC; 3 cm: n päässä T1
• TP = 308,2K = 35,2 ºC; 4 cm: n päässä T1

Viitteet

1. Figueroa, D. 2005. Sarja: Tieteen ja tekniikan fysiikka. Nide 5. Nesteet ja termodynamiikka. Toimittanut Douglas Figueroa (USB).
2. Kirkpatrick, L. 2007. Fysiikka: Katsaus maailmaan. Kuudes lyhennetty painos. Cengage -oppiminen.
3. Makaa, j. 2004. Suunnittelijoiden yleinen fysiikka. Laitos.
4. Mott, r. 2006. Fluidimekaniikka. Neljäs. Painos. Pearson -koulutus. 
5. Strangeways, minä. 2003. Luonnollisen ympäristön mittaus. Toinen. Painos. Cambridge University Press.
6. Wikipedia. Lämmönjohtokyky. Palautettu: on.Wikipedia.com