Fourier -muunnosominaisuudet, sovellukset, esimerkit

Se Fourier Transform Se on integroitaviin toimintoihin suunnattu analyyttisen riittävyyden menetelmä, joka kuuluu T -perheellekattava reunustettu. Se koostuu toimintojen uudelleenmäärittelystä F t) COS (t) ja Sen (t): n (t) suhteen.

Näiden funktioiden trigonometriset identiteetit yhdessä niiden johdannaisen ja antitointiominaisuuksien kanssa määrittelee Fourierin muunnos seuraavan kompleksin funktion kautta:

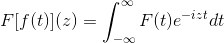
Joka täyttyy, kun ilmaisu on järkevää, ts. Kun väärä integraali on lähentävä. Algebrallisesti sanotaan, että Fourier's Transform on lineaarinen homeomorfismi.

Mikä tahansa funktio, jota voidaan työskennellä Fourier -muunnoksen kanssa, on oltava mitätöisyys määritetyn parametrin ulkopuolella.

[TOC]

Ominaisuudet

Lähde: Pexels

Fourier -muunnos vastaa seuraavia ominaisuuksia:

Olemassaolo

Fourier -muunnoksen olemassaolon varmistamiseksi kuninkaallisissa määriteltyksi f (t) -funktioksi R -, Seuraavat 2 aksiomia on täytettävä:

1. f (t) on jatkuvaa palasiksi kaikesta R -
2. f (t) on integroitavissa R -

Fourier -muunnos lineaarisuus

Olkoon m (t) ja n (t) kaksi kahta toimintoa määritellyn Fourier -transformoituna, vakioilla A ja B mikä tahansa.

F [a m (t) + b n (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)

Joka perustuu myös saman nimen integraalin lineaarisuuteen.

Fourier muuttui johdannaisesta

Sinulla on toiminto F  joka on jatkuvaa ja integroitavaa kaikissa REAISissa, missä:

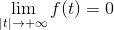
Ja johdannainen F (f ') Se on jatkuva ja määritelty paloiksi kaikessa R -

Johdannaisen Fourier -muunnos määritellään integroimalla osilla seuraavalla lausekkeella:

F [f '(t)] (z) = izF [f (t)] (z)

Korkeamman asteen johdannaisissa sitä sovelletaan homologisella tavalla, missä sinun on kaikille n 1:

F [f ⁿ'(t)] (z) = (iz)ⁿF [f (t)] (z)

Fourier -muunnoksen erottelu

Sinulla on toiminto F  joka on jatkuvaa ja integroitavaa kaikissa REAISissa, missä:

I (d/dz)F [f (t)] (z) = F  [t .  f (t)] (z)

Fourier muuttui käännöksestä

Kaikille θ joka kuuluu sarjaan ja T Se kuuluu sarjaan, sinun on:

F [ τ_-lla θ] =  ja^-Iay F [[ θ]                                 F [ τ_-llaT ] =  ja^-Iax  F [[ T]   

Kanssa  τ_-lla  työskentelee vektorin käännösoperaattorina.

Fourier -muunnoksen käännös

Kaikille θ joka kuuluu sarjaan ja T Se kuuluu sarjaan, sinun on:

τ_-lla F [θ] =  F [ja^-Iax.θ]                                τ_-lla F [t ] =  F [ja^-Iay . T]

Voi palvella sinua: Hypercubo: Määritelmä, mitat, koordinaatit, taitetut

Kaikille -lla joka kuuluu R -

Asteikon ryhmän Fourier -muunnos

Kaikille θ joka kuuluu sarjaan S. T Se kuuluu sarjaan S '

λ kuulua R - 0  Sinun täytyy:

F [θ (λx)] = (1 / | λ |) F [θ] (ja/λ-A                 

F [T (λx)] = (1 / | λ |) F [T] (ja/λ-A

Joo F Se on jatkuva ja puhtaasti integroitava toiminto, jossa A> 0. Niin:

F [f (at)] (z) =   (1/a) F [f (t)] (z/a) 

Tämän tuloksen osoittamiseksi voimme jatkaa muuttujan muutosta.

Kun t → + sitten s = at → + ∞

Kun t → - sitten s = at → - ∞

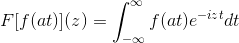
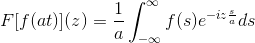
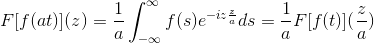
Symmetria

Fourier Transforman symmetrian tutkimiseksi.

Sinulla on θ ja δ, jotka kuuluvat S. Sieltä voidaan päätellä, että:

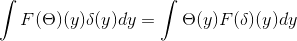
Saada

1 / (2π)^{d -d}  F [θ ], F [Δ- Parseval -identiteetti

1 / (2π)^D/2  || F [θ - ||_Lens²_{R -}^{d -d}     Plancherel -kaava

Fourier muuttui tuotteesta konvoluutioksi

Jahtaamalla samanlaisia ​​tavoitteita, jotka Laplace -muunnossa toimintojen konvoluutio viittaa tuotteeseen sen Fourier -muunnosten joukossa.

Siinä on F ja G 2 funktion rajoitettu, määritelty ja täysin integroitava:

F (f *g) = f (f) . F (g)

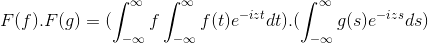
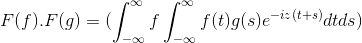
Sitten muuttujan muutos

t + s = x; Kaksinkertainen integraali kaksinkertainen integraali jatkuu

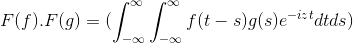
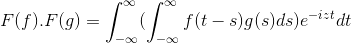
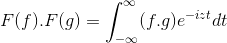
F (f) . F (g) = f (f . g)

Jatkuvuus ja putoaminen äärettömyydessä

Kaikille θ, joka kuuluu R, F [ θ] noudattaa jatkuvan funktion kriteerejä rajoitettuna R: ssä^{d -d}.

Myös F [ θ] (y) → 0 C si | y | → ∞

Historia

Tämän matemaattisen konseptin esitteli Joseph B. Fourier vuonna 1811 kehitettäessä sopimusta Lämmön leviäminen. Se ottivat sen nopeasti käyttöön eri tieteen ja tekniikan sivukonttorit.

Se perustettiin päätyökaluna tutkiessaan yhtälöitä osittaisten johdannaisten kanssa, vertaamalla jopa työsuhteita Laplace Transformated ja tavalliset differentiaaliyhtälöt.

Mikä on Fourier -muunnos?

Se palvelee pääasiassa merkittäviä yhtälöitä, kun taas voimaelementeiksi johdettuja lausekkeita muuntavat, jotka merkitsevät erilaisia ​​lausekkeita integroitavien polynomien muodossa.

Tulosten optimoinnissa, moduloinnissa ja mallintamisessa se toimii standardisoiduna lausekkeena, joka on usein tekniikan resurssi useiden sukupolvien jälkeen.

Fourierin sarja

Ne ovat määriteltyjä sarjoja kasenin ja rintojen suhteen; Ne auttavat helpottamaan työtä yleisten jaksollisten toimintojen kanssa. Sovellettuna ne ovat osa osittaisten ja tavallisten differentiaaliyhtälöiden resoluutiotekniikoita.

Se voi palvella sinua: todellinen todellisen muuttujan toiminto ja sen graafinen esitys

Fourier -sarja on vielä yleisempi kuin Taylorin sarja, koska ne kehittävät jaksollisia disontinua -funktioita, joilla ei ole esitystä Taylor -sarjassa.

Fourier -sarjan muut muodot

Analyyttisesti ymmärtää Fourier -muunnos on tärkeää.

-Fourier -sarja 2L -jakson toiminnolla

Monta kertaa on tarpeen mukauttaa Fourier-sarjan rakenne, jaksollisiin toimintoihin, joiden ajanjakso on p = 2L> 0 aikavälillä [-l, l].

-Fourier -sarja tasaisina ja parittomissa toiminnoissa

Aika [-π, π] otetaan huomioon, joka tarjoaa etuja funktioiden symmetristen ominaisuuksien hyväksi.

Jos F on vääntömomentti, Fourier -sarja on perustettu sarjanaan Cosenos.

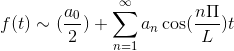
Jos F on outoa, Fourier -sarja on perustettu rintojen sarjana.

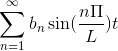
-Fourier -sarjan monimutkainen merkintä

Jos sinulla on f (t) -toiminto, joka täyttää kaikki Fourier-sarjan kehitetyt vaatimukset, on mahdollista merkitä se aikavälillä [-t, t] sen monimutkaisen merkinnän avulla:

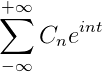
Sovellukset

Lähde: Pexels

Perusratkaisun laskeminen

Fourier's Transform on tehokas työkalu tutkimaan lineaarisen tyypin osittaisia ​​differentiaaliyhtälöitä vakiokertoimilla. Hakeudu toimintoihin, joilla on verkkotunnuksia, ei rajoitettu tasaisesti.

Kuten Laplace -muunnos, Fourier -muunnos muuttaa osittaisten johdannaisten funktion tavalliseksi differentiaaliyhtälöksi, joka on paljon helpompi käyttää.

Cauchyn lämpöyhtälön ongelma esittelee Fourier -muunnoksen usein levityskentän, jossa funktio luodaan Dirichlet -lämpö tai ydin ydin.

Perusratkaisun laskemisesta esitetään seuraavat tapaukset, joissa on yleistä löytää Fourier -muunnos:

-Laplace -yhtälö

-Lämpöyhtälö

-Schrödinger -yhtälö

-Aaltoyhtälö

Signaaliteoria

Yleinen syy Fourier -muunnoksen soveltamiseen tässä haarassa johtuu lähinnä signaalin ominaishajoamisesta äärettömänä päällekkäisyytenä helpommin hoidettavien signaalien päällekkäisyytenä.

Se voi olla ääniaalto tai sähkömagneettinen aalto, Fourier -muunnos ilmaisee sen yksinkertaisilla aaltoilla. Tämä esitys on melko usein sähkötekniikassa.

Voi palvella sinua: Pystysuora viiva

Toisaalta ne ovat esimerkkejä Fourier -muunnoksen soveltamisesta signaaliteorian kentällä:

-Järjestelmän tunnistusongelmat. Perustettu f ja g

-Ongelma lähtösignaalin johdonmukaisuudessa

-Ongelmat signaalin suodatuksessa

Esimerkit

Esimerkki 1

Määritä seuraavan lausekkeen Fourier -muunnos:

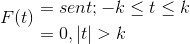
Voimme myös edustaa sitä seuraavasti:

F (t) = Synti (t) [h_{(T + k)} - H_{(T - k)} -

Suorakulmainen pulssi on määritelty:

p (t) = h_{(T + k)} - H_{(T - k)}

Seuraavaan lausekkeeseen sovelletaan Fourier -muunnosta, joka muistuttaa modulaatiolausetta.

f (t) = p (t) sin (t)

Missä: F [W] = (1/2) i [P (W + 1) - P (W - 1)]

Ja Fourier -muunnos määritellään:

F [W] =  (1/2) i [(2/2W+1) Sen (K (W+1)) - (2/2W+1) Sen (K (W-1))]

Esimerkki 2

Määritä Fourier -muunnos ilmaisua varten:

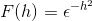Määritelmän mukaan ilmaisemme muunnon seuraavasti

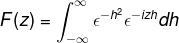
Koska f (h) on tasainen funktio, se voidaan vahvistaa

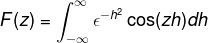Julkaisu integraalissa Z: n suhteen, lauseke voidaan kirjoittaa uudelleen. Tämä vaihe on merkittävä työssä erotusyhtälöiden kanssa.

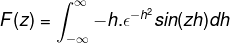
Osien integrointia käytetään valitsemalla muuttujat ja niiden erot seuraavasti

u = sin (zh) du = z cos (zh) dh

dv = h (e^-h-A²                       V = (e^-h-A² / 2

Sen korvaaminen

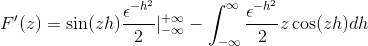
Arvioinnin jälkeen laskelman peruslauseen nojalla

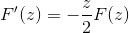
Ensimmäisen järjestyksen differentiaaliyhtälöihin liittyvää aikaisempaa tietoa soveltamalla lauseke on merkitty

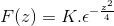
Saadaksesi k arvioimme 

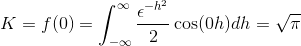
Lopuksi Fourierin muuntaminen määritellään

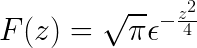
Ehdotetut harjoitukset

• Määritä lauseke Fourier -muunnos
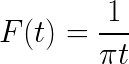
• Ratkaise seuraava virheellinen integraali käyttämällä Paresvalsin tasa -arvoa
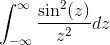
• Hanki lausekkeen muunnos w/(1+W²-A

Viitteet

1. Duoandikoetxea zuazo, j., Fourier -analyysi. Addison-Wesley Iberoamericana, Madridin autonominen yliopisto, 1995.
2. Lionit, j. Lens., Matemaattinen analyysi ja numeeriset menetelmät tieteen ja tekniikan kannalta. Springer-Verlag, 1990.
3. Lieb, E. H., Gaussin ytimissä on vain Gaussin maksimoijia. Keksiä. Matematiikka. 102, 179-208, 1990.
4. Dym, h., McKean, H. P., Fourier -sarja ja integraalit. Academic Press, New York, 1972.
5. Schwartz, L., Théorie des -jakelu. Ed. Hermann, Pariisi, 1966.