Ominaisuudet vino kolmiot, esimerkit, harjoitukset

Se Vino kolmio He ovat niitä, joilla ei ole suorakulmaa, joten mikään heidän sisäkulmistaan ​​ei ole yhtä suuri kuin 90º. Joten vino kolmio voi olla Akuttaa tai tylppä.

Ensimmäisessä tapauksessa kolmion sisäkulmat ovat akuutteja tai mikä on sama: alle 90º, kun taas toisessa on aina yli 90º kulma, ts. Katsotaanpa esimerkkiä jokaisesta seuraavassa kuvassa:

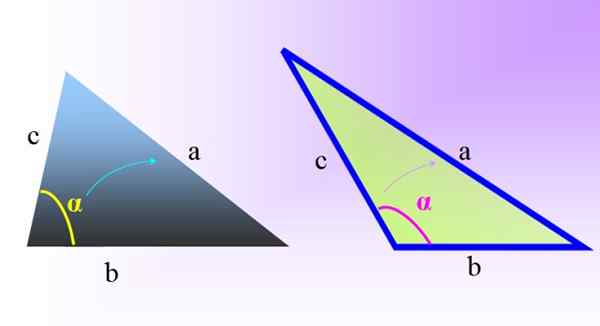Kuvio 1. Oblek -kolmiot: Vasemmalla vinossa ja acutlangle -kolmiossa. Oikealla vinossa ja tylsässä kolmiossa. Lähde: f. Zapata.

Sivujen pituudet ja tällaisten kolmioiden sisäkulmien mittaukset suorat kulmat puuttuen Pythagoras -lausetta ei ole mahdollista käyttää.

Kolmion ratkaisemiseksi on kuitenkin vaihtoehtoja: kosinin ja rinnan lauseet ja se, että sisäkulmien summa on yhtä suuri kuin 180º.

[TOC]

Oblicuágulos -kolmiot esimerkkejä

Oppaan itseämme kuvassa 1, voimme helposti tunnistaa vinot kolmiot kahden kriteerin avulla, jotka annamme alla.

Acutangle -kolmio

Olla sivujen A, B ja C kolmio, α -kulma sivun edessä.

Jos akuutin kulman α vastakkaisen sivun neliö on pienempi kuin jäljellä olevien sivujen neliöiden summa, kolmio on acutlangle. Algebrallisesti:

-lla² < b² + c²; α < 90º

Suhteellinen tasa -arvoinen kolmio, joka on saman mittaan kolme puolta, on acutlangle ja siksi vino, koska sen sisäkulmat ovat yhtä suuret ja mitat 60º.

Sotkuinen kolmio

Toisaalta, jos neliö vastakkaisella puolella -lla Tyhjennä kulmassa α on suurempi kuin kahden muun neliöiden summa, olemme tylsä ​​kolmion läsnä ollessa. Siksi:

-lla² > b² + c²; α> 90º

Esimerkiksi kolmio, jonka sisäkulmat ovat 105º, 60º ja 15º, on tylsä ​​vino kolmio. Huomaa, että 105º + 60º + 15º = 180º.

Sinuksen ja kosinin lauseet

Viblik -kolmioiden ratkaisemiseksi, toisin sanoen kaikkien niiden sivujen ja kaikkien kulmien mitat, rintojen ja kosinin lauseet vaaditaan.

Olkoon kolmion a, b ja c, ja α, β ja y niiden sisäiset kulmat. Niin:

Rintojen lause

Rintalause vahvistaa seuraavan:

Jos α on vastakkainen kulma kuin sivu A, β on kulma, joka on sivua B ja γ, sivun C edessä oleva kulma.

Se voi palvella sinua: Antidervative: Kaavat ja yhtälöt, esimerkit, harjoitukset

Vastaava:

Päätämme soveltaa rintalausetta, kun aiomme ratkaista kolmion kuin enemmän kulmia tunnetaan kuin puolet.

Coseno -lause

Coseno -lauseen mukaan:

c² = a² + b -² - 2⋅ A⋅B⋅Cos γ

Jälleen kulma γ on sivun c edessä. Voimme myös kirjoittaa vastaavia lausekkeita sivuille A ja B, seuraavasti:

-lla² = b² + c² - 2⋅B⋅C⋅Cos α

JA

b -² = a² + c² - 2⋅ A⋅C⋅Cos β

Kosininlausetta sovelletaan mieluiten, kun kahden puolen arvo ja niiden välinen kulma tunnetaan. Lisäksi kun kolmion kolme sivua on tiedossa, lause antaa meille mahdollisuuden laskea kahden välisen kulman kosiini.

Ratkaisut

- Harjoitus 1

Tarkista, että kolmio, jonka sivut mittaavat 20, 10 ja 12 mielivaltaisia ​​yksiköitä, on tylsä.

Ratkaisu

Emme tunne mitään sisäkulmista, mutta kriteerien mukaan, jotka tunnistavat tylsöiset kolmiot, voimme nostaa epätasa -arvoa sivujen neliöiden kanssa tarkkailemaan, jos se täyttyy.

Ensin löydämme neliöt molemmilta puolilta:

kaksikymmentä² = 400

10² = 100

12² = 144

Ja näemme sen todella: 400> 100 + 144, 400> 244: n jälkeen. Siksi kolmio sisältää yli 90º: n kulman, joka sijaitsee sivun edessä, joka mittaa 20. Näin ollen tämä kolmio on vino lisäksi.

- Harjoitus 2

Kun otetaan huomioon kuvassa 2 esitetty vino kolmio, jonka mittaukset on annettu mielivaltaisina yksiköissä, määritä:

a) x: n arvo. Onko se acutlangle vai tylppä kolmio?

b) kolmion jäljellä olevat sisäkulmat

c) kehä

d) alue.

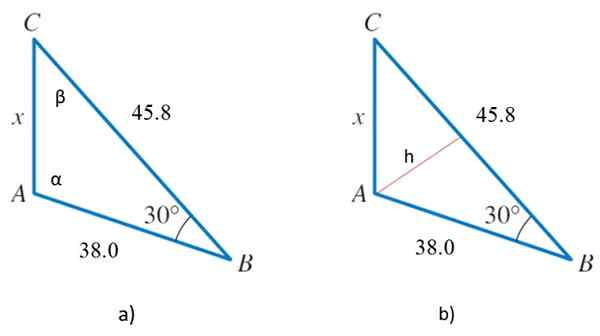Kuva 2. 2A) Vuoden kolmio ratkaistiin 2 ja 2b) sama kolmio, jolla on korkeus, joka auttaa alueen määrittämistä. Lähde: f. Zapata.

Liittää jhk

Kolmiosta tunnetaan kaksi vierekkäistä puolta, joiden mitat ovat 38.0 ja 45.8 ja niiden välinen kulma, joka on 30º, siten kosinin lause on välittömästi käytetty:

x² = 38.0 -² + Neljä viisi.8² - 2 x 38.0 x 45.8 x cos 30º = 527.18

Siksi:

x = (527.18)^1/2 = 22.96

Piirustus viittaa siihen, että α> 90º ja kolmio on tylsä, vinojen lisäksi. Tarkastellaksesi sitä löydämme sivujen neliöt, kuten edellisessä harjoituksessa tehtiin:

22.96² = 527.18

38.0 -² = 1444.00

Neljä viisi.8² = 2097.64

Kulma α on suurempi kuin 90º, jos se on totta kuin vastakkaisen puolen neliö: 45.8²  Se on suurempi kuin muiden osapuolten neliöiden summa, joka on 22.96² + 38.0 -².

Voi palvella sinua: Eksponenttien lait

Katsotaanpa, tapahtuuko niin:

527.18 + 1444.00 = 1971.2

Todellakin:

2097.64> 1971.2

Siksi kulma α on suurempi kuin 90º.

Ratkaisu b

Nyt voimme soveltaa rintalausetta löytääksemme yhden puuttuvista kulmista. Aiomme nostaa sen kulmaan β:

SEN 30º / 22.96 = sin β / 38

SEN β = 38 x (SEN 30º / 22.96) = 0.8275

β = Arcsen (0.8275) = 55.84º

Puuttuva kulma voidaan löytää tietäen, että minkä tahansa kolmion sisäkulmien summa on 180º. Siksi:

55.84º + 30º + α = 180º

α = 94.16º

Jos haluat, voit myös käyttää kosininlausetta löytääksesi kulman kosinin, joka on kahden vierekkäisen sivun välissä. Kun Coseno -kaari -toimintoa käytetään kulman määrittämiseen.

Tulokset voivat poiketa hiukan desimaaleissa, tehdyn pyöristämisen mukaan.

Liuos C

Ympäristö P on kuvion ääriviivat, mikä vastaa kolmen puolen mittojen summaa:

P = 22.96 + 38.00 + 45.80 = 106.76 mielivaltaista yksikköä.

Liuos D

Kaava minkä tahansa kolmion alueen laskemiseksi on:

A = (1/2) x emäs x korkeus

Meidän on valittava yksi sivusta pohjaksi ja määritettävä korkeus. Esimerkiksi valitsemalla sivu, joka mittaa 45.8, piirrämme korkeuden h kunnes kärki A, joka on kuvion 2b punainen viiva.

Tämän tekemällä jakaamme alkuperäisen kolmion kahteen suorakulmuun, molemmat h Yleisenä katetona. Mikä tahansa heistä palvelee, koska tiedämme terävän sivun ja kulman.

Aiomme ottaa sen, jolla on hypotenusa yhtä suuri kuin 38, luokka, joka mittaa h, joka on etsitty korkeus ja akuutti kulma yhtä suuri kuin 30º.

Akuutin kulman 30º trigonometristen syiden avulla määritämme arvon h-

SEN 30º = Cateto vastapäätä 30º / hypotenusa = H / 38

H = 38 x Sen 30º = 19

Siksi:

A = (1/2) x 45.8 x 19 = 435.1 mielivaltaiset alueen alueet.

Olisimme voineet valita toisen puolen pohjaksi, esimerkiksi puolella 38, siinä tapauksessa korkeus h Se on erilainen, koska muodostuu toinen suorakaiteen kolmio, mutta alueen tulos on sama. Se on edelleen harjoitus, jotta lukija tarkistaa sen.

- Harjoitus 3

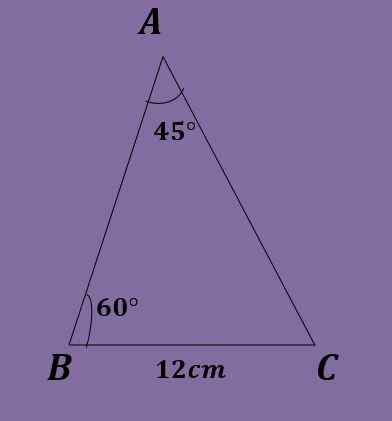
Annetaan ABC -kolmio, jonka A = 45º, B = 60º ja A = 12 cm, laske toinen kolmiotiedot.

Voi palvella sinua: ryhmittelyn merkkejä

Ratkaisu

Kolmion sisäkulmien summan käyttäminen on yhtä suuri kuin 180º, sen on:

C = 180º-45º-60º = 75º.

Kolme kulmaa on jo tiedossa. Sitten siirrymme rintalakiin puuttuvien osapuolten laskemiseen.

Nousevat yhtälöt ovat 12 / ilman (45º) = b / ilman (60º) = c / ilman (75º).

Ensimmäisestä tasa -arvosta voit tyhjentää "B" ja saada sen:

B = 12*ilman (60º)/ilman (45º) = 6√6 ≈ 14.696cm.

Voit myös tyhjentää "C" ja saada sen:

C = 12*sin (75º)/sin (45º) = 6 (1+√3) ≈ 16.392cm.

- Harjoitus 4

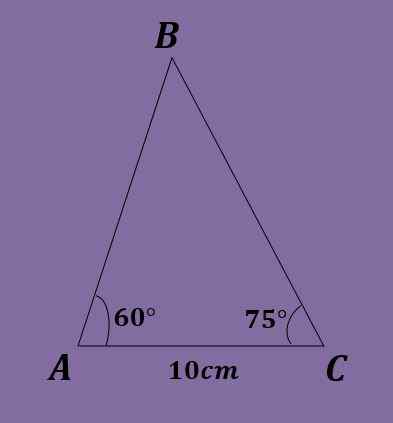
Ottaen huomioon kolmio ABC siten, että A = 60º, C = 75º ja B = 10 cm, laske toinen kolmiotiedot.

Ratkaisu

Kuten edellisenä vuonna, sinun on b = 180º-60º-75º = 45º. Lisäksi sinun on käytettävä rintalaki / ilman (60º) = 10 / ilman (45º) = c / ilman (75º), missä saadaan, että a = 10*ilman (60º) / ilman (45º) = 5 √6 ≈ 12.247 cm ja c = 10*sin (75º)/ilman (45º) = 5 (1+√3) ≈ 13.660 cm.

- Harjoitus 5

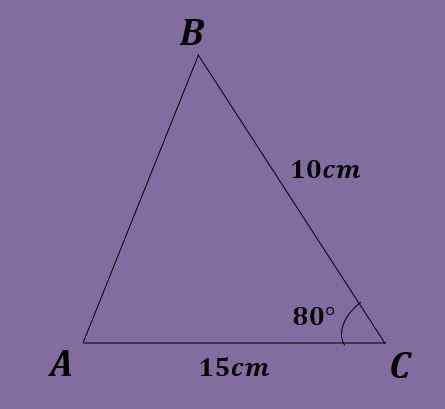
Ottaen huomioon kolmio ABC siten, että A = 10 cm, B = 15 cm ja c = 80º, laske toinen kolmiotiedot.

Ratkaisu

Tässä harjoituksessa tiedetään vain kulma, joten se ei ole mahdollista aloittaa, kuten se tehtiin kahdessa aiemmassa harjoituksessa. Lisäksi rintalakia ei voida soveltaa, koska yhtälöä ei voitu ratkaista.

Siksi sovelletaan kosenosin lakia. Sinun täytyy:

C² = 10²+15² - 2 (10) (15) cos (80º) = 325 - 300*0.173 ≈ 272.905 cm,

Niin että c ≈ 16.51 cm. Nyt kun tiedät 3 puolta, rintalaki käytetään ja saadaan, että:

10 / ilman (a) = 15 / ilman (b) = 16.51 cm /ilman (80º).

Tästä lähtien, kun kirkas b on ilman (b) = 15*ilman (80º)/ 16.51 ≈ 0.894, mikä tarkoittaa, että b ≈ 63.38º.

Nyt voidaan saada, että A = 180º - 80º - 63.38º ≈ 36.62º.

- Harjoitus 6

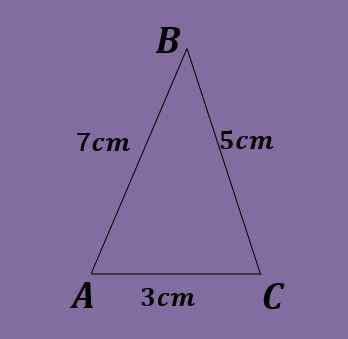
Viblique -kolmion sivut ovat A = 5cm, B = 3cm ja C = 7cm. Laske kolmion kulmat.

Ratkaisu

Jälleen rintoja koskevaa lakia ei voida soveltaa suoraan, koska mikään yhtälö ei halua saada kulmien arvoa.

Kosinin lakia käyttämällä sinun on c² = a² + b² - 2ab cos (c), mistä cos (c) = (a² + b² - c²)/ 2ab = (5² + 3² -7²)/ 2*5 *3 = -15/30 = -1/2 ja siksi c = 120º.

Nyt rintalaki voidaan soveltaa ja siten saada 5/ilman (a) = 3/ilman (b) = 7/ilman (120º), missä B voidaan puhdistaa b ja saada se ilman (b) = 3* ilman (120º )/7 = 0.371, niin että b = 21.79º.

Lopuksi viimeinen kulma lasketaan käyttämällä A = 180º-130º-21.79º = 38.21.

Viitteet

1. Clemens, S. Geometria sovelluksilla. Addison Wesley.
2. Ibáñez, P. 2010. Matematiikka III. Cengage -oppiminen.
3. Jiménez, r. Matematiikka II: Geometria ja trigonometria. Toinen. Painos. Pearson.
4. Matematiikka sinulle. Sotkuinen kolmio. Toipunut: matematiikka.WordPress.com.
5. Stewart, J. 2007. Ennakkoluulo. Viides. Painos. Cengage -oppiminen.