Eräs romboidi Se on neljän sivun litteä hahmo, -kvadrilateral -in, jonka sivut ja sen sisäkulmat ovat erilaisia ​​kahdesta kahteen. Siksi rhboidi kuuluu vinojen rinnakkaisten ryhmiin.

Geometriset hahmot ovat osa luontoa ja erityisesti neljän puolen, kuten rhboidia, on monia sovelluksia arkkitehtuurissa ja suunnittelussa.

Kuvio 1. Allianz Arenan stadionin valaistuspaneelit Münchenissä, Saksassa, valaisevat paikallisen joukkueen värejä ja valkoisella valolla, kun kyseisen maan valinta. Lähde: Pxhere.

Ylös meillä on osa Münchenin Allianz Arenan jalkapallostadionin julkisivua. Ne ovat romboidipaneeleja, jotka syttyvät paikallisen joukkueen väreissä.

Siksi se on kuva, jolla on paljon visuaalista dynaamisuutta, koska toisin kuin muut kvadrilateraalit, sillä ei ole symmetria -akselia. Seuraava kuva näyttää erilaisia ​​rhomboideja, joiden tasossa on monipuolinen suuntaus.

Kuva 2. Useita rhomboidia, joilla on erilaisia ​​suuntauksia tasossa. Lähde: f. Zapata.

[TOC]

Romboid -ominaisuudet

Seuraavaksi tämän mielenkiintoisen geometrisen hahmon pääpiirteet:

-Arkin numero: 4.

-Verkkojen lukumäärä: 4.

-Vastakkaiset puolet ovat samat ja yhdensuuntaiset, mutta viereiset sivut ovat epätasa -arvoisia.

-Siinä on 4 sisäkulmaa: kaksi akuuttia (alle 90º), merkitty kreikkalaisella kirjaimella α ja kahdella otoskulla (yli 180º), nimeltään β (katso kuva 3).

-Lisäämällä kaksi vierekkäistä kulmaa romboidista, saadaan 180º, siksi a ja β ovat Lisä-.

-4 sisäkulman summa on yhtä suuri kuin 360º.

-Diagonaali on segmentti, joka alkaa kärkipisteestä ja päättyy vastakkaisella kärkillä.

-Pistettä, jolloin rhboidun leikkaus diagonaalit kutsutaan barycenter.

-Rhomboidia diagonaaleilla on erikokoisia.

Rhomboidin diagonaaleista on joitain tärkeitä yksityiskohtia, joista keskustelemme alla.

Voi palvella sinua: Rivin odottaminen: Kaava ja yhtälöt, esitys, esimerkit

Romboidi diagonaalit

On erittäin tärkeää korostaa, että rhboidien diagonaalit eivät ole bisektrisiä, ts. Ne eivät jaa kuvion sisäkulmat kahteen yhtä suureen osaan.

Diagonaalit eivät ole kohtisuorassa toisiinsa nähden. Voimme kuitenkin helposti laskea ne kosinuslauseella. Siten tärkein diagonaali d_M Kuvion 3 rhomboidissa on:

D -d_M = √ (a² + b -² - 2.Ab.cos β)

Ja pieni diagonaali d_m Minä olisin:

D -d_m = √ (a² + b -² - 2.Ab.cos α)

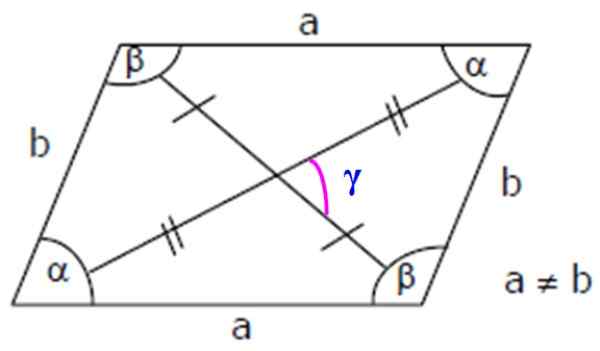Kuva 3. Romboid -elementit: sivut, sisäiset ja diagonaalikulmat. Lähde: Wikimedia Commons.

Tärkeä: Kuten α ja β ovat täydentäviä, on täytettävä, että:

sin α = sin β

cos α = -cos β

Nämä trigonometristen syiden ominaisuudet on otettava huomioon harjoitusten ratkaisemisessa.

Kuinka poistaa kehä ja alue

Kään ja alueen löytämiseksi annamme nimen rhboidun sivuille, nämä ovat -lla ja b -. Meillä on myös rhboidun korkeus, nimeltään h, joka on viiva, joka on piirretty yhdestä kärjestä ja suunnattu kohtisuoraan kuvan vastakkaiselle puolelle.

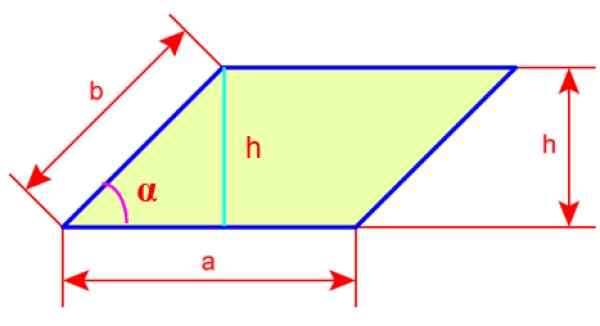Kuva 4. Sivut ja rhomboidikorkeus. Lähde: Wikimedia Commons.

Rhomboidi

Rhomboidin kehä lasketaan lisäämällä sen neljän sivun pituudet. Soitetaan P kehälle, sitten:

P = 2a + 2b

Voimme myös ilmaista sen läpi:

P = 2 (a+b)

Kehä tietäen korkeuden

Jos näytämme hyvältä, korkeus H voidaan määrittää kuvan 4 vasemmalla puolella olevasta kolmiosta. Side B olisi hypotenuse ja korkeus H Cateto vastustaa kulmaa α, siksi:

sin α = vastapäätä / hypotenusa catoto

O No:

sin α = h / b

Sitten puhdistamme b:

b = h / sin α

Korvaamme kehällä p:

P = 2 [a + (h / sin α)]

Romboid -alue

Rhomboidialue on sen pinnan mitta. Ja koska se on rinnakkaisohjelma, sen pinta -ala A annetaan hyvin tunnetulla lausekkeella:

Voi palvella sinua: Yleinen tekijä ryhmittelyssä: Esimerkkejä, harjoituksia

A = pohja x korkeus

Että kuvien 3 ja 4 mukaan se ilmaistaan:

A = a x h

Alue tuntee molemmat osapuolet ja sisäkulma

Soveltamalla edellisen jakson trigonometriaa, löydämme vastaavat lausekkeet romboidialueelle:

h = b. synti α

Sitten alue on näin:

A = a. b -. synti α

Muistamme sen, mitä edellä sanoimme lisäkulmista, voimme korvata Sen α: n tarvittaessa SEN β: lla.

Alue tuntee diagonaalit ja kulma niiden välillä

Lopuksi, jos tiedämme diagonaalit d_M ja D_m, Lisäksi niiden välinen kulma y (katso kuva 3), pinta -ala voidaan laskea diagonaalien puolijalotuotteella mainitun kulman rinnan läpi:

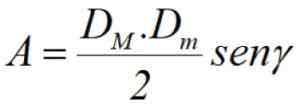
Liikuntaa

Seuraavassa rhomboidissa, jonka mitat on annettu mielivaltaisissa yksiköissä tai.-lla., löytö:

a) kehäarvo

b) alue

c) Sisäiset kulmat α ja β

d) RX -segmentin pituus

e) kunkin diagonaalin mitta

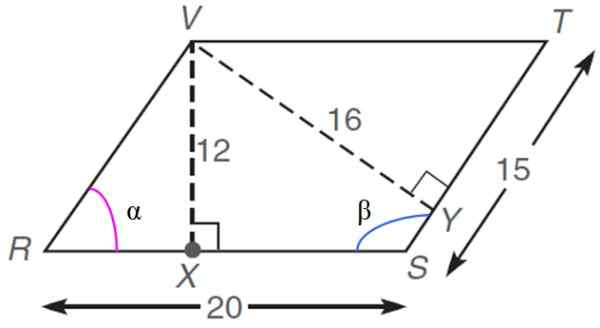
Liittää jhk

Ympäristö P on:

P = 2 (a + b)

Tunnistamme ensin A: n ja B: n arvot:

A = 20

B = 15

Korvaamme kaavan ja laskemme:

P = 2. (20 + 15) = 70 U.-lla.

Ratkaisu b

Kaavio tarjoaa korkeuden h = 12 u.A, siksi alue voidaan laskea kaavalla:

A = a x h

A = 20 x 12 u.-lla.² = 240 U.-lla.²

Valittuista yksiköistä riippumatta sivujen ja korkeuden mittaamiseksi, alue ilmaistaan ​​aina neliöyksiköinä.

Sama tulos, jos saat laskettaessa aluetta rhboidin toisella korkeudella, joka on 16 U: n arvoinen.-lla. Todellakin:

A = 16 x 15 u.-lla.² = 240 U.-lla.²

Liuos C

Kulma α voidaan laskea:

Se voi palvella sinua: sijaintitoimenpiteet, keskeinen taipumus ja leviäminen

h = b. synti α

Koska H- ja B -arvot tunnetaan, siksi:

α = Arcsen (H/B) = Arcsen (12/15) = 53.13. päivä

Muistaen, että α- ja β -kulmat ovat täydennettyjä:

α + β = 180º ⇒ β = 180 - 53.13. = 126.87º

Liuos D

RX -segmentin pituus lasketaan helposti, koska sitä on riittävästi tietoa. Esimerkiksi:

Rx = matkailuauto . cos α = 15 . Cos 53.13. u.-lla. = 9 u.-lla.

Myös Pythagoras -lauseen läpi sivujen 15 ja 12 u suorakulmion kolmion läpi.MÄÄN:

(RV)² = (RX)² + h²

Kiinnostussegmentin pituuden puhdistaminen:

Rx = √ [(RV)² - h²] = √ [15² - 12²] = √81 = 9

Ratkaisu E

Yhden diagonaalien mitta, esimerkiksi kärjessä R- ja T liittyvä diagonaali, joka on merkittävä diagonaali, antaa kosinin lause, kuten aiemmin selitettiin, joten korvaamme arvot siellä:

D -d_M = √ (20² + 25² - 2. kaksikymmentä. viisitoista .Cos 126.87º) = 37.22 u.-lla.

Pienelle diagonaalille:

D -d_m = √ (20² + 25² - 2. kaksikymmentä. viisitoista .Cos 53.13.) = 25.79 U.-lla.

Viitteet

1. Alexander, D. 2013. Geometria. Viides. Painos. Cengage -oppiminen.
2. Baldor, a. 1973. Geometria ja trigonometria. Keski -Amerikan kulttuuritoimitus.
3. JA. -Lla. 2003. Geometriaelementit: harjoituksilla ja kompassin geometrialla. Medellinin yliopisto.
4. Jiménez, r. 2010. Matematiikka II. Geometria ja trigonometria. Toinen painos. Prentice Hall.
5. Tavallinen monikulmikone. Toipunut: kaveri.tekniikka.USAC.Edu.GT.
6. Maailmankaikkeuden kaavat. Romboidi. Toipunut: UniversOformulat.com.
7. Wikipedia. Romboidi. Palautettu: on.Wikipedia.org.