Lineaarinen variaatiokonsepti, esimerkit, liikunta ratkaistu

Se Lineaarinen variaatio Se tapahtuu kahden fyysisen suuruuden välillä, kun niitä edustava kaavio on suora. Se vastaa vakuuttamista, että muuttujat ovat lineaarisessa riippuvuudessa, joten jos joku niistä kutsumme sitä "y" ja toiseksi "x", ne liittyvät matemaattisella ilmaisulla:

y = mx + b

Tässä kaavassa M ja B ovat todellisia lukuja. M: n arvo edustaa viivan kaltevuutta tai kaltevuutta - joka on aina vakio - ja B on linjan leikkaus pystysuoran akselin kanssa.

Yhden suuruuden lineaarinen variaatio suhteessa toiseen tarkoittaa, että sen kuvaaja on suora. Lähde: Joulesergio/CC BY-S (https: // creativecommons.Org/lisenssit/by-SA/4.0)

Jokaisella lineaariseen variaatioon reagoiva ilmiöllä on erilaiset nimet muuttujille, kuten seuraavissa esimerkeissä näemme. Yhtälön matemaattinen muoto on kuitenkin sama.

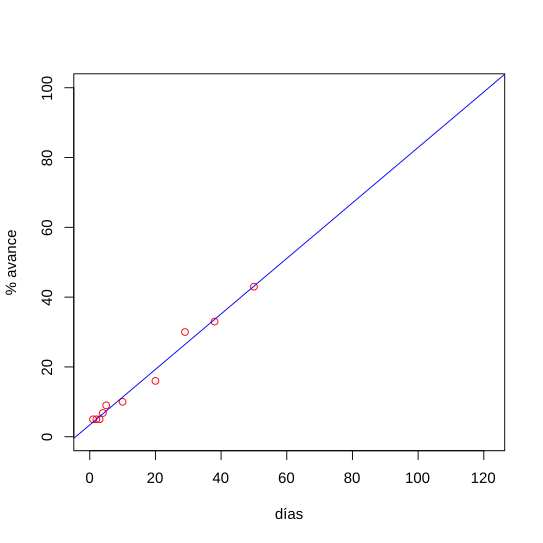
Kokeellisesti voidaan määrittää, jos kahden suuruuden välillä on lineaarinen suhde, arvoparien mittaaminen (x, y).

Saadut kohdat ovat graafisia millimetrin paperissa ja niitä havaitaan, jos niillä on lineaarinen suuntaus, ts. Jos on olemassa viiva, joka sopeutetaan riittävästi kokeelliseen tietoon.

Ensinnäkin tämä viiva voidaan piirtää visuaalisesti, mutta a lineaarinen regressio Niitä voidaan löytää analyyttisesti, linjan M ja B arvot, jotka sopivat parhaiten kokeellisiin pisteisiin.

[TOC]

Esimerkkejä lineaarisesta variaatiosta

Luonnollisia ilmiöitä on lukuisia ja vakiintuneita suhteita mittausmallien välillä, jotka noudattavat esimerkiksi lineaarista variaatiota:

Nopeus tasaisesti vaihtelevassa suoraviivaisessa liikkeessä

Nopeus riippuen matkapuhelimen ajasta v (t), joka liikkuu pitkin linjaa pitkin jatkuvaa kiihtyvyyttä AT: lla ja alkuperäisen nopeuden V_jompikumpi  erilainen kuin 0. Tämä liike tunnetaan nimellä tasaisesti monipuolinen suoraviivainen liike Ja nopeusyhtälö on:

Voi palvella sinua: tiheys

v (t) = v_jompikumpi + At

Lämpölaajeneminen

Toinen luonnollinen ilmiö, jonka variaatio on lineaarinen, on pituuden lisääntyminen, joka kokee sauvan tai langan kuumennettaessa.

Itse asiassa, kun minkä tahansa esineen lämpötila nousee, myös sen mitat ja tämä nousu riippuu lämpötilan muutoksesta ΔT ja nimeltään määrästä lineaarinen dilaatiokerroin merkitty kreikkalaisella kirjaimella α:

L = l_jompikumpi + α AT

Tässä lausekkeessa L on objektin ja L lopullinen pituus_jompikumpi on sen alkuperäinen pituus.

Matkapuhelimen sijainti, jolla on jatkuva nopeus

Liikkua jkn kanssa nopeus vakio liikkuu aina suorassa linjassa. Jos suora viiva on vaaka -akseli X, sijainti x (t) milloin tahansa annetaan:

x (t) = x_jompikumpi + VT

Missä x_jompikumpi Se on alkupaikka, v on nopeus ja t on aika. Tällä tavalla sanotaan, että x -sijainti vaihtelee lineaarisesti ajan t.

Henkilö

Lääkärit ja antropologit voivat arvioida ihmisen aseman mittaamalla reisiluun pituus.

Mitä korkeampi henkilö, sitä pidempään jaloilla on, joten on lineaarisia malleja ennustaa aikuisen ihmisen H (tuumina), jos sen reisiluun pituus L (myös tuumina) tunnetaan yhtälön mukaan:

H = 1.880⋅L + 32.010

Lämpötila -asteikot

Celsius- ja Fahrenheit -asteikkoja käytetään päivittäin lämpötilojen mittaamiseen. Tätä viimeistä asteikkoa käytetään yleisesti englanninkielisissä maissa. On vastaavuus siirtyä yhdestä toiseen:

F = (9/5) C + 32

Missä F on lämpötila asteina Fahrenheit ja C on lämpötila celsiusasteissa.

Paine ja syvyys

Absoluuttinen paine P puristamattomassa nesteessä, kuten vedessä, jonka vakiotiheys on ρ, vaihtelee syvyyden H mukaan:

Se voi palvella sinua: Vaaka -ammunta: Ominaisuudet, kaavat ja yhtälöt, harjoitukset

P = p_jompikumpi + ρgh

Missä p_jompikumpi Se on nesteen vapaan pinnan paine. Jos neste on ilmakehään avoimessa säiliössä, tämä paine on yksinkertaisesti ilmakehän paine P_{Pankkiautomaatti}, Mahdollisuus kirjoittaa sitten:

P = p_{Pankkiautomaatti} + ρgh

Ilmakehän paine merenpinnassa on noin 101 kPa. Tämä suhde P: n ja H: n välillä tarkoittaa, että paine kasvaa lineaarisesti syvyyden kanssa.

Sukeltajan kokenut paine vaihtelee lineaarisesti syvyyden mukaan. Lähde: Ahmed Samy/Pexels.

Liikuntaa

Ajokustannukset

Auton käsittelyn kuukausittaiset kustannukset C sisältää kuukausittaiset kiinteät kustannukset c_jompikumpi plus mittarilukema tai mittarilukema kulki joka kuukausi. Kuljettaja huomauttaa, että kuukaudessa hallintokustannukset olivat 380 dollaria 480 dollarilla, ja seuraavana kuukautena se oli 460 dollaria 800 mailia kohti.

Olkoon kuljettaja kuukaudessa kulkea mailia kuukaudessa, ja löydä: Etsi:

a) lineaarinen variaatio C: n ja D: n välillä.

b) Paljonko auto maksaa kuukaudessa 1500 mailin matkalla?

c) c -kaavio vs. d.

Liittää jhk

Oletetaan, että muuttujilla on suhde:

C = c_jompikumpi + -Lla.d -d

Missä a ja c_jompikumpi Ne ovat vakioita määrittämään. A on linjan kaltevuus, joka graafisesti edustaa C: n ja D: n välistä suhdetta. CO on leikkaus pystysuoralla akselilla, kuukausittaiset kiinteät kustannukset, jotka kuljettajan on maksettava pelkästään auton saatavilla olevasta tosiasiasta. Täällä ylläpito- ja verokustannukset voitaisiin sisällyttää esimerkiksi.

Linjan yksiselitteisesti määrittämiseksi on tarpeen tietää sen kaltevuus. Tätä varten meillä on pisteet:

P₁: 480 mailia, 380 dollaria

P₂: 800 mailia, 460 dollaria

Nämä koordinaattien (d, c) tai (etäisyys, kustannukset) kohdat ovat analogisia Cartesian -tason koordinaattipisteiden kanssa (x, y), mitkä muutokset ovat nimet. Linjan kaltevuus on sitten:

Voi palvella sinua: kalteva taso

A = (c₂ - C₁)/(D₂ - d -d₁-A

A = [(460 - 380) $ / (800 - 480) mailia] = (1/4) $ / maili

Linjan kaltevuus edustaa tällä tavalla kustannuksia mailia kohti:

C = c_jompikumpi + -Lla.D = Co + (1/4).d -d

Peruskustannusten c määrittäminen C_jompikumpi Tämä yhtälö otetaan ja yksi tuntemistamme kohdista kuuluu siihen, esimerkiksi P₁-

380 $ = C_jompikumpi + [(1/4) $ / maili] . 480 mailia → 380 $ = C_jompikumpi + 120 dollaria

C_jompikumpi = 260 dollaria

Nyt voimme muotoilla lineaarisen variaatiomallin, kuten:

C = 260 + (1/4) d

Ratkaisu b

1500 mailin matkustamisen kuukausittaiset kustannukset ovat:

C = 260 + (1/4) x 1500 $ = 635 dollaria

Liuos C

C: n kuvaaja d: n funktiona on:

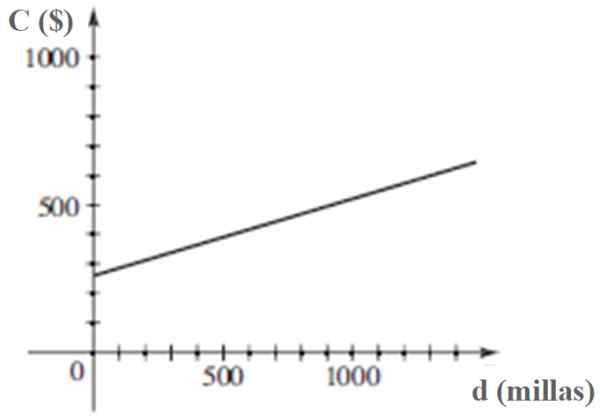Ajoneuvon käsittelyn kustannus C on kuljetetun D: n lineaarinen toiminta. Lähde: Stewart, J. Ennakkoluulo.

Viitteet

1. Kalju. 1977. Perusalgebra. Venezuelan kulttuuriversiot.
2. Hoekenga, c. Lineaariset yhtälöt tieteessä. Toipunut: VisionLearning.com.
3. Hoffman, J. Matematiikan aiheiden valinta. Nide 2.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
6. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.