Varustevektorit Määritelmä, merkintä, harjoitukset

Kaksi tai useampi Vektorit ovat laitteita Jos heillä on sama moduuli, sama suunta ja yhtä suuri merkitys, jopa silloin, kun heidän alkuperäpiste on erilainen. Muista. 

Vektorit edustavat suuntautuneen tai nuolen segmentin. Kuvio 1 esittää useiden vektoreiden esityksen tasossa, joista osa on alun perin annettujen määritelmän mukaan laitteita.

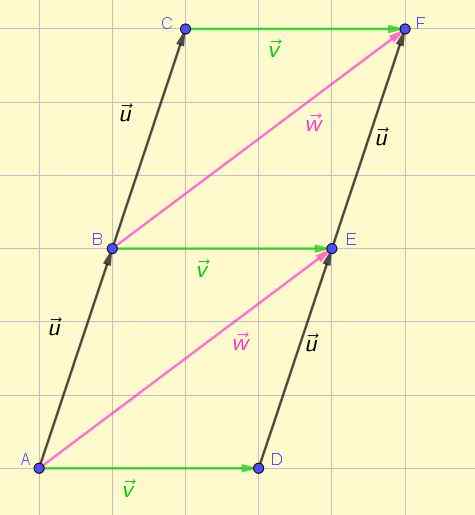Kuvio 1. Laitteet ja vaatimattomat vektorit. Lähde: Itse tehty.

Ensi silmäyksestä on mahdollista arvostaa, että kolmella vihreällä vektorilla on samankokoinen, sama suunta ja sama merkitys. Sama voidaan vahvistaa kahden vaaleanpunaisen vektorin ja neljän mustan vektorin ympärillä.

Lukuisilla luonnon suuruuksilla on vektorikäyttäytyminen, kuten nopeus, kiihtyvyys ja lujuus, vain joitain mainita. Siten niiden karakterisoinnin merkitys.

[TOC]

Vektorien ja laitteiden merkintä

Skalaarien määrien vektorimäärien erottamiseksi kirjaimen mustan tyyppistä kirjainta tai nuolta käytetään usein. Kun työskentelet käsikirjassa käsikirjassa, on välttämätöntä erottaa ne nuolella ja kun käytetään tulostettua välinettä, käytetään lihavoituja.

Vektorit voidaan kieltää osoittaen heidän lähtökohtansa tai alkuperänsä ja saapumispisteensä. Esimerkiksi Ab, BC, - ja EF kuvio 1 ovat kuitenkin vektoreita Ab, BC, - ja EF Ne ovat skalaarisia määriä tai numeroita, jotka osoittavat vastaavien vektorien suuruuden, moduulin tai koon.

Osoittaakseen, että kaksi vektoria on laitteita, symbolia käytetään "∼ ". Tällä merkinnällä voimme tuoda esiin seuraavat vektorit, jotka ovat laitteita keskenään:

Voi palvella sinua: Kineettinen energia: Ominaisuudet, tyypit, esimerkit, harjoitukset

Ab∼BC∼DE - Ef 

Heillä kaikilla on sama suuruus, suunta ja merkitys. Siksi noudattaa edellä mainittuja määräyksiä.

Vapaat, liukuvat ja vastakkaiset vektorit

Mikä tahansa kuvan vektoria (esimerkiksi Ab) on edustaja kaikkien kiinteiden kiinteiden vektorien joukosta. Tämä ääretön sarja määrittelee vapaiden vektorien luokan tai.

tai = AB, BC, From, EF, ..

Vaihtoehtoinen merkintä on seuraava:

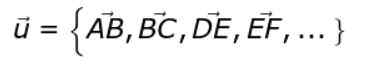
Jos rohkeaa tai nuolta ei ole asetettu päälle tai, Haluamme viitata vektorimoduuliin tai.

Ilmaisia ​​vektoreita ei sovelleta tiettyyn kohtaan.

Heidän puolestaan Liukuvektorit Ne ovat laitteita tietylle vektorille, mutta niiden levityspiste on oltava Vector -toimintalinjassa.

Ja vastakkaiset vektorit Ne ovat vektoreita, joilla on sama suuruus ja suunta, mutta vastakkaiset aistit, vaikka niitä kutsutaan englanniksi vastakkaiset osoitteet Koska osoite osoittaa myös merkityksen. Vastakkaiset vektorit eivät ole laitteita.

Harjoitukset

-Harjoitus 1

Mitkä muut kuvassa 1 esitetyt vektorit ovat laitteita toistensa kanssa?

Ratkaisu

Edellisessä osassa jo ilmoitettujen lisäksi kuvasta 1 havaitaan, että ILMOITUS, Olla ja EY Ne ovat myös varustevektoreita toisiinsa:

AD ∼ on ∼ CE 

Jokainen heistä edustaa ilmaisten vektorien luokkaa v.

Vektorit ovat myös laitteita keskenään Ae ja Bf -

AE ∼ Bf 

Jotka ovat luokan edustajia W -.

-Harjoitus 2

Pisteet A, B ja C ovat Cartesian XY -lentokoneessa ja niiden koordinaatit ovat:

Voi palvella sinua: Ihanteellinen kaasu: malli, käyttäytyminen, esimerkit

A = (-4,1), b = (-1,4) ja c = (-4, -3)

Etsi neljännen pisteen D koordinaatit niin, että vektorit Ab ja CD Olla laitteita.

Ratkaisu 

Jotta CD olla laitteita Ab on oltava sama moduuli ja sama suunta kuin Ab .

Moduuli Ab Neliö on:

JaAb|^2 = (-1 -( -4))^2 + (4 -1)^2 = 9 + 9 = 18

D -koordinaatteja ei tunneta siitä, mitä voimme sanoa: d = (x, y)

Sitten: |CD|^2 = (x -(-4))^2 + (y -( -3))^2

As |Ab| = |CDJa Se on yksi ehdoista Ab ja CD Ole laitteet, jotka sinulla on:

(x + 4)^2 + (y + 3)^2 = 18

Koska tuntemattomia on kaksi, vaaditaan toinen yhtälö, joka voidaan saavuttaa siitä tilasta, että Ab ja CD olla samanaikainen ja samassa mielessä.

Vektori ab -kaltevuus

Vektorikalte Ab Ilmaisee osoitteesi:

Odottaa ab = (4 -1)/(-1 -( -4)) = 3/3 = 1

Osoittaa, että vektori Ab Muoto 45º X -akselilla.

CD -vektorikarte

Rinne CD Se lasketaan samalla tavalla:

Odottavat CD = (y -( -3))/(x -(-4)) = (y + 3)/(x + 4)

Vastaa tätä tulosta rinteellä Ab Sinulla on seuraava yhtälö:

Y + 3 = x + 4 

Mikä tarkoittaa y = x + 1.

Jos tämä tulos korvataan moduulien tasa -arvon yhtälössä, se on:

(x + 4)^2 + (x + 1 + 3)^2 = 18

Yksinkertaistaminen on:

2 (x+4)^2 = 18, 

Mikä vastaa:

(x+4)^2 = 9

Se on x+4 = 3, mikä tarkoittaa, että x = -1. Niin että D: n koordinaatit ovat (-1, 0).

tarkistaa

Vektorikomponentit Ab Ne ovat (-1-(-4); 4 -1) = (3; 3)

Voi palvella sinua: Thévenin -lause: mitä koostuu, sovellukset ja esimerkit

ja vektorin CD ne ovat (-1-(-4)); 0 -(-3)) = (3; 3)

Mikä tarkoittaa, että vektorit ovat laitteita. Jos kahdella vektorilla on samat Cartesian -komponentit ovat samat moduulit ja suunnat, siksi ne ovat laitteita.

-Harjoitus 3

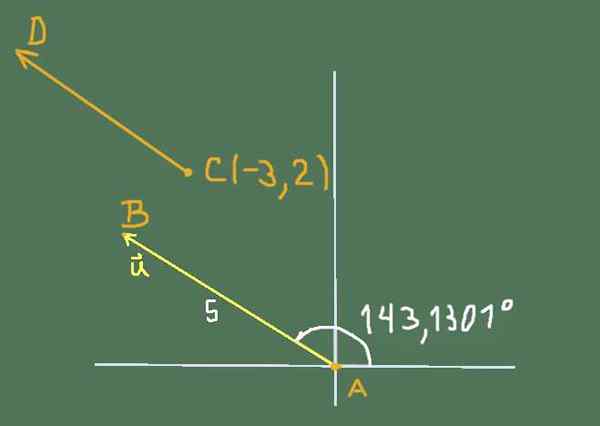
Ilmainen vektori tai on suuruusluokka 5 ja osoite 143 1301º.

Löydä sen Cartesian -komponentit ja määritä pisteiden B ja C koordinaatit tietäen, että kiinteät vektorit AB ja CD ovat laitteita. A: n koordinaatit ovat (0, 0) ja pisteen C koordinaatit ovat (-3,2).

Ratkaisu 

Harjoituksen ehdottama tilanne voidaan edustaa seuraavassa kuvassa:

Kuva 2. Kaavio harjoituksen 3 ratkaisemiseksi. Lähde: Itse tehty.

Kartesian komponentit tai are

tai = (5*cos (143 1301º); 5*sin (143 1301º))) 

Laskelmien tekeminen on edelleen:

tai = (-4; 3) 

B -koordinaatteja ei tunneta, joten asetamme B (x, y)

Vektorin koordinaatit Ab Ne ovat (X-0; Y-0), mutta koska se on u: n laitteita, on täytettävä komponenttien tasa-arvo, siksi päätellään, että B: n koordinaatit ovat (-4, 3).

Samoin vektorikoordinaatit CD ne ovat (x-(-3)); (ja - 2) sen on oltava laitteita u, lTai se johtaa:

 x + 3 = -4 ja y -2 = 3

Sitten pisteen D koordinaatit ovat (-7, 5).

Viitteet

1. Laskeminen.DC. Kiinteä vektori. Ilmainen vektori. Palautettu: laskelma.DC
2. 2d Descartes. Kiinteät vektorit ja vapaita vektoreita. Haettu: Resurssit.koulutus.On
3. Guao -projekti. Varustevektorit. Toipunut: guao.org
4. Resnick, r., Krane, k. (2001). Fysiikka (englanniksi). New York: John Wiley & Sons.
5. Serway, R.; Jewett, John W. (2004). Fysiikka tutkijoille ja insinööreille (englanniksi) (6. painos). Brooks/Cole.
6. Tukler, Paul A. (2000). Fysiikka tieteen ja tekniikan puolesta. Osa. Barcelona: Ed. Käännyin.
7. Weisstein, E. "Vektori". Weissteinissä, Eric W. Mathworld (englanniksi). Wolfram -tutkimus.