Välitön nopeuden määritelmä, kaava, laskenta ja harjoitukset

Se välitön nopeus Se määritellään siirtymän välittömänä muutoksena ajan myötä. Se on käsite, joka lisää suurta tarkkuutta liikkeen tutkimukseen. Ja se on etukäteen keskimääräisen nopeuden suhteen, jonka tiedot ovat hyvin yleisiä.

Saadaksesi hetkellisen nopeuden, katsotaanpa mahdollisimman pienen aikavälin. Differentiaalinen laskenta on täydellinen työkalu tämän idean ilmaisemiseen matemaattisesti.

Välitön nopeus on matkapuhelimen nopeus jokaisessa reitin kohdassa. Lähde: Pixabay.

Lähtökohta on keskimääräinen nopeus:

Nyt tehdään Δt -lähestymistapa 0: een, mikä voi. Tämä on raja ja tulos on juuri hetkellinen nopeus:

Tämä raja tunnetaan johdannaisen nimellä. Differentiaalilaskennassa: sinulla on:

Edellyttäen, että liike on rajoitettu suoralle linjalle, se voidaan antaa vektorimerkinnällä.

[TOC]

Välitön nopeuden laskenta: geometrinen tulkinta

Seuraava kuva näyttää johdannaisen käsitteen geometrisen tulkinnan: se on linjan kaltevuus tangentti Käyrä x (t) vs. t Jokaisessa vaiheessa.

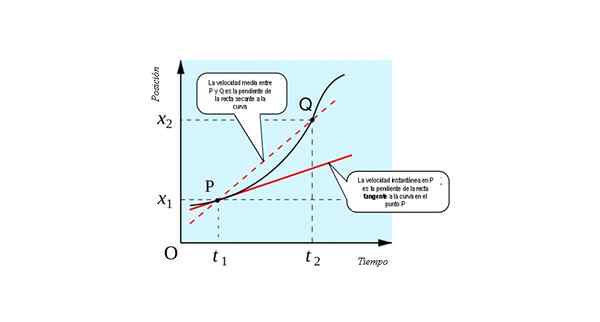P -ekvivalentin välitön nopeus numeerisesti linjan kaltevuuteen tangenttia käyrälle X Vs. t kohdassa P. Lähde: Lähde: すじにく シチュー [CC0].

Voit kuvitella kuinka saada raja, jos piste q lähestyy vähitellen. Tulee aika, jolloin molemmat kohdat ovat niin lähellä, että henkilöä ei voida erottaa toisesta.

Heitä yhdistävä linja kuivuu (suora, joka leikkaa kahteen pisteeseen) tangentiksi (suora, joka koskettaa käyrää yhdessä pisteessä). Siksi liikkuvan hiukkasen hetkellisen nopeuden löytämiseksi meidän pitäisi olla:

• Kaavio hiukkasten sijainnista ajan funktiona. Löydät käyrän tangentin kaltevuus jokaisen ajankohtana, sinulla on hetkellinen nopeus jokaisessa hiukkasen käyttämässä pisteessä.

Voi palvella sinua: Ampère Law: Formula ja yhtälöt, esittely, harjoitukset

O No:

• Hiukkasten sijaintitoiminto x (t), joka on johdettu nopeusfunktion saamiseksi V (t), Sitten tämä toiminto arvioidaan joka kerta t, Mukavuus. Paikkatoiminnon oletetaan olevan johdettavissa.

Jotkut erityistapaukset hetkellisen nopeuden laskennassa

-P -käyrän tangentti viivan kaltevuus on 0. Noll -kaltevuus tarkoittaa, että matkapuhelin pysäytetään ja että sen nopeus on tietysti 0.

-P -käyrän tangenttiviivan kaltevuus on suurempi kuin 0. Nopeus on positiivinen. Yllä olevassa kaaviossa se tarkoittaa, että matkapuhelin siirtyy pois tai.

-P -käyrän tangenttiviivan kaltevuus on alle 0. Nopeus olisi negatiivinen. Yllä olevassa kaaviossa ei ole sellaisia ​​kohtia, mutta siinä tapauksessa hiukkas lähestyy tai.

-Käyrän tangentti linjan kaltevuus on vakio P: ssä ja kaikissa muissa kohdissa. Tässä tapauksessa kaavio on suora ja matkapuhelimella yhtenäinen linjaliike MRU (sen nopeus on vakio).

Yleensä toiminto V (t) Se on myös aikafunktio, joka puolestaan ​​on voinut johtaa. Entä jos ei olisi mahdollista löytää funktioista johdettuja x (t) ja V (t)?

Siinä tapauksessa että x (t) Voi olla, että kaltevuus - hetkellinen nopeus - muutti merkkejä jyrkästi. Tai se siirtyy nollasta toiseen arvoon välittömästi.

Jos niin, grafiikka x (t) Se esittäisi vinkkejä tai kulmia äkillisissä muutoksissa. Hyvin erilainen kuin edellisessä kuvassa esitetty tapaus, jossa käyrä x (t) Se on pehmeä käyrä, ilman pisteitä, kulmia, epäjatkuvuuksia tai äkillisiä muutoksia.

Voi palvella sinua: Bose Einstein Condensate

Totuus on, että todellisille matkapuhelimille pehmeät käyrät ovat ne, jotka edustavat parhaiten esineen käyttäytymistä.

Yleinen liike on melko monimutkainen. Mobiili voidaan pysäyttää jonkin aikaa, kiihtyä liikkumaan lepoon nopeuden ja päästäksesi pois lähtökohdasta, pidä nopeus hetkeksi, lopeta sitten pysähtyä uudelleen ja siten tyyli.

He voivat aloittaa uudelleen ja jatkaa samaan suuntaan. Tai toimi takaisku ja paluu. Tätä kutsutaan monipuoliseksi liikkeeksi ulottuvuudessa.

Alla joitain esimerkkejä hetkellisen nopeuden laskemisesta selventää annetun määritelmän käyttöä:

Ratkaistuja välittömiä nopeusharjoituksia

Harjoitus 1

Hiukkas liikkuu suoraa linjaa pitkin seuraavan liikkeen lain kanssa:

x (t) = -t³ + 2 t² + 6 t - 10

Kaikki yksiköt ovat kansainvälisessä järjestelmässä. Löytö:

a) hiukkasen sijainti t = 3 sekunnissa.

b) Keskimääräinen nopeus välin välillä t = 0 s ja t = 3 s.

c) Keskimääräinen nopeus välin välillä t = 0 s ja t = 3 s.

d) Edellisen kysymyksen hiukkasen hetkellinen nopeus, t = 1 s.

Vastaukset

a) Löydä hiukkasen sijainti, liikuntalaki (sijaintitoiminto) t = 3:

x (3) = (-4/3).3³ + 2. 3² ₊ 6.3 - 10 m = -10 m

Ei ole mitään ongelmaa, että sijainti on negatiivinen. Merkki (-) osoittaa, että hiukkas on alkuperän vasemmalla puolella tai.

b) Keskimääräisen nopeuden laskennassa hiukkasen lopulliset ja alkupaikat vaaditaan ilmoitetuina aikoina: x (3) ja x (0). Asema t = 3 on x (3) ja tunnetaan edellisestä tuloksesta. Asema t = 0 sekunnissa on x (0) = -10 m.

Voi palvella sinua: staattinen: historia, mitä tutkimuksia, sovelluksia, lakeja

Koska lopullinen sijainti on sama kuin alkuperäinen, on heti päätetty, että keskimääräinen nopeus on 0.

c) Keskimääräinen nopeus on syy kuljetetun etäisyyden ja käytetyn ajan välillä. Nyt etäisyys on siirtymän moduuli tai suuruus, siksi:

Etäisyys = | x2 - x1 | = | -10-(-10) | M = 20 m

Huomaa, että kuljetettu etäisyys on aina positiivinen.

v_{M = 20 m/3 s = 6.7 m/s}

d) Täältä on tarpeen löytää ensimmäinen aseman johdannainen aika. Sitten se arvioidaan t = 1 sekunnin ajan.

x '(t) = -4 t² + 4 t + 6

x '(1) = -4.1² + 4.1 + 6 m/s = 6 m/s

Harjoitus 2

Alla on kaavio matkapuhelimen sijainnista ajan funktiona. Löydä hetkellinen nopeus t = 2 sekunnissa.

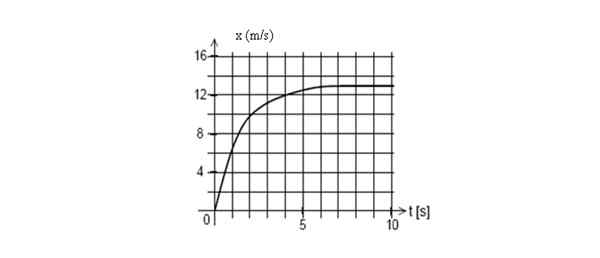Sijoita kuvaaja verrattuna matkapuhelimeen. Lähde: Itse tehty.

Vastaus

Piirrä tangenttiviiva käyrään t = 2 sekunnissa, laske sitten kaltevuus, ottaen kaksi pistettä linjasta.

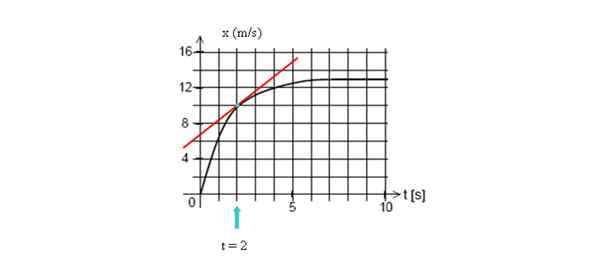Piirrä tangenttiviiva siihen pisteeseen ja löydä sen kaltevuus. Lähde: Itse tehty.

Tässä esimerkissä otamme kaksi pistettä, jotka on helposti visualisoitu, joiden koordinaatit ovat (2 s, 10 m) ja leikkaus pystysuoralla akselilla (0 s, 7 m):

Viitteet

1. Giancoli, D. Fysiikka. Periaatteet hakemuksissa. 6^th Painos. Prentice Hall. 22-25.
2. Resnick, r. (1999). Fyysinen. Osa 1. Kolmas painos espanjaksi. Meksiko. Mannertoimitusyhtiö S.-Lla. C: n.V. 21-22.
3. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. 7^mehu. Painos. Meksiko. Cengage Learning Editors. 23-25.