Yleinen Parabola -yhtälö (esimerkit ja harjoitukset)

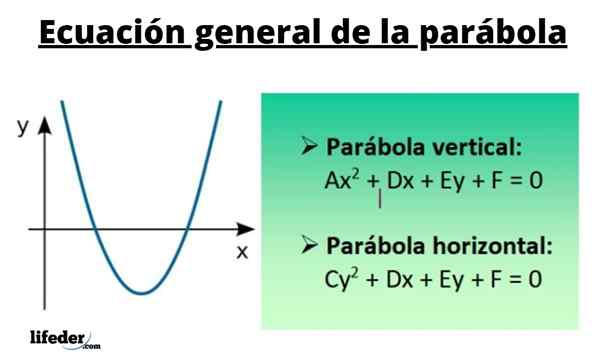
Se Vertaus yleinen yhtälö sisältää neliömäisiä termejä vuonna x ja sisään ja, samoin kuin lineaariset termit molemmissa muuttujissa sekä riippumaton termi. Ensimmäinen symmetria -akseli on yhdensuuntainen pystysuuntaisen akselin kanssa ja toisen vaakasuuntainen akseli.

Yleensä neliömäinen yhtälö, josta puuttuu ristetty termi Xy Se on kirjoitettu seuraavasti:

Kirves² + Kierto² +Dx + ey + f = 0

A, C, D, E ja F arvot ovat reaalilukuja. Edellytysten asettaminen ∙ c = 0 ja a+c ≠ 0, käyrä, joka johtuu tämän yhtälön tyydyttävien pisteiden piirtämisestä, on parabola.

Tapaus 1

Pystysuoraan vertaukseen sen yleinen yhtälö on:

Kirves² + Dx + ey + f = 0

Missä a ja e eroavat 0: sta. Toisin sanoen, kun termi ilmestyy x: n kanssa², Vertaus on pystysuora.

Tapaus 2

Puolestaan ​​vaakasuuntaiselle vertaukselle sinulla on:

Kierto² + Dx + ey + f = 0

Tässä C ja D eroavat myös 0: sta, siksi neliöllinen termi vastaa ja vastaa².

Joka tapauksessa vertauksen yleinen yhtälö on neliöllinen yhdessä muuttujissa ja lineaarinen toisessa.

Vertauselementit

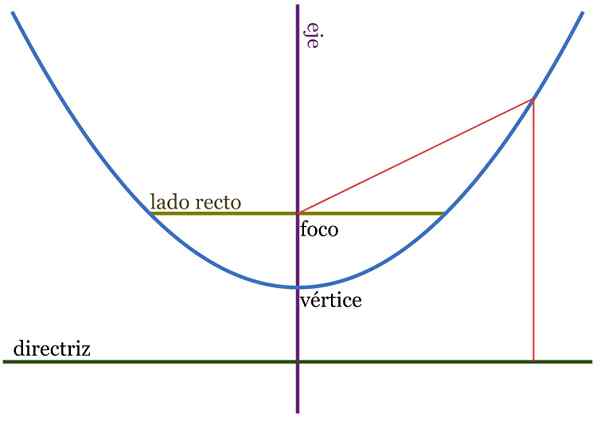Kuva 2. Vertauselementit. Etäisyydet QF ja QH ovat yhtä suuret. Lähde: Wikimedia Commons.

Geometriseksi paikkaksi määritelty parabola koostuu yhden tason pisteiden joukosta, jotka rinnastavat toisesta kohdasta nimeltään keskittyä Ja myös linja, joka tunnetaan nimellä suora ohje.

Yleisen yhtälön perusteella on mahdollista tutkia vertausta määrittelemällä sen elementit. Sisältää keskittymisen ja ohjeen, nämä elementit, jotka on kuvattu lyhyesti, ovat:

-Akseli, jotka viittaavat parabolin symmetria -akseliin, voi olla vaakasuora (abskissan akselin yhdensuuntainen) tai pystysuuntainen (yhdensuuntainen ordinaattien akselin kanssa).

Voi palvella sinua: Yleinen tekijä ryhmittelyssä: Esimerkkejä, harjoituksia

-Suuntautuminen, joka puolestaan ​​vastaa akselin suuntausta. Vertaus on pystysuora, jos sen symmetria -akseli on pystysuora, ja se on vaakasuora, kun myös akseli on.

-Kärki, Se on kohta, jossa akseli leikkaa vertauksen.

-Keskittyä, Akselilla sijaitseva piste, vertauksen sisällä ja etäisyydellä p kärjestä. Parabolan kaikki kohdat ovat yhtä mieltä suuntaviivan keskittymistä ja suuntausta.

-Parametri, Se on etäisyys p Painopisteen ja kärjen välillä.

-Suora ohje, joka on kohtisuorassa Y -akseliin ja myös etäisyyteen p vertauksen kärkipisteestä, mutta ei leikkaa sitä, koska se on ulkopuolella.

-Suorakulma, Köysi kulkee keskittymisen läpi, leikkaa vertauksen kahdessa pisteessä, kohtisuorassa sen akseliin nähden.

-Epäkeskeisyys, että parabolan tapauksessa se on aina 1 arvoinen.

-Graafinen esitys.

Tiedot kaikkien näiden elementtien määrittämiseksi sisältyy yleiseen yhtälöön.

Kanoninen muoto

Parabolan elementtien määrittämiseksi on joskus kätevää siirtää yleinen muoto saman muodon kaanoniseen muotoon, neliömäisen muuttujan neliöiden loppuun saattamisella.

Tämä kanoninen muoto on:

(X-H)² = 4p (y-k)

Missä piste (h, k) on vertauksen kärkipiste V. Yleisen yhtälön kanonisesta muodosta voi tulla myös merkittävän tuotteen kehittäminen ja termien järjestäminen uudelleen.

Esimerkit

Esimerkki 1

Seuraavat ovat Parabola -yhtälöitä yleensä:

a) 4x² + 5y - 3 = 0

b) 1 - 2y + 3x -ja² = 0

A) kertoimet tunnistetaan: a = 4, c = 0, d = 0, e = 5, f = -3. Se on vertaus, jonka symmetria -akseli on pystysuora.

Voi palvella sinua: synteettinen jako

Puolestaan ​​b) yleinen yhtälö on edelleen:

- ja² + 3x - 2y + 1 = 0

Ja kertoimet ovat: c = -1, d = 3, e = -2 ja f = 1.

Esimerkki 2

Seuraava vertaus on kanonisessa muodossa:

(Y-1)² = 6 (x-3)

Yleisen yhtälön löytämiseksi huomattava tuote on kehitetty ja sulku suoritetaan oikealla:

ja² -2y + 1 = 6x -18

Nyt kaikki vasemmalla olevat ehdot ohitetaan ja ne on ryhmitelty kätevästi:

ja² -2y + 1- 6x +18 = 0 → ja² - 6x -2y + 19 = 0

Kuten neliöllinen termi on ja² Se on vaakasuora vertaus. Kertoimet ovat:

C = 1; D = -6; E = -2, f = 19.

Ratkaisut

Harjoitus 1

Seuraava vertaus on yleensä annettu:

x² -10x -12y - 11 = 0

Sitä pyydetään kirjoittamaan se kanonisessa muodossa.

Ratkaisu

Mene kanoniseen muotoon saavutetaan suorittamalla neliöt, tässä tapauksessa muuttuja X. X: n termit alkavat suluissa:

(x² -10x) -12y - 11 = 0

Sinun on muutettava suluissa täydelliseksi neliömäiseksi trinomiksi, joka saavutetaan lisäämällä 5², Se luonnollisesti on vähennettävä, koska muuten lauseke muuttuu. Se pysyy näin:

(x² −10x+5²) −12Y - 11–5²= 0

Sulujen kolme termiä muodostavat täydellisen neliön trinomia (x-5)². Se voidaan tarkistaa kehittämällä tämä merkittävä tuote vahvistaaksesi. Nyt vertaus jäänteet:

(X-5)² -12y -36 = 0

Seuraava on ottaa huomioon sulujen ulkopuolella olevat termit:

(X-5)² -12 (y +3) = 0

Se muuttuu lopulta:

(X-5)² = 12 (y +3)

Esimerkki 2

Etsi edellisen vertauksen elementit ja rakenna grafiikka.

Ratkaisu

Kärki

Parabolan kärkillä on koordinaatit V (5, -3)

Se voi palvella sinua: hepagonaalinen prisma

Akseli

Rivi x = 5.

Parametri

Parametriarvosta p joka näkyy kanonisessa muodossa: (x-h)² = 4p (y-k) vertaa molempia yhtälöitä:

4P = 12

P = 12/4 = 3

Suuntautuminen

Tämä vertaus on pystysuora ja avautuu. Koska kärkipiste sijaitsee x = 5, y = -3, symmetrian akseli on pystysuora viiva x = 5.

Keskittyä

Painopiste on rivillä x = 5, siksi sillä on myös koordinaatti x = 5.

Koordinaatti ja painopisteen on oltava p-yksiköitä K: n yläpuolella, ts. P + K = 3 + (-3) = 0, sitten tarkennus on pisteessä (5.0).

Suora ohje

Se on kohtisuorassa akseliin nähden, joten se on muodoltaan y = c, nyt, kun etäisyys p kärjestä on kaukana, mutta vertauksen ulkopuolella se tarkoittaa, että se on etäisyydellä p k: n alapuolella:

y = k -p = -3-3 = -6

Suorakulma

Tämä segmentti leikkaa vertauksen, kulkee tarkennuksen läpi ja on suuntaviivan suuntainen, siksi se sisältyy linjaan y = 0.

Graafinen esitys

Se voidaan hankkia helposti ilmaisista online -grafiikkaohjelmistoista, kuten geogebra. Sisäänkäynnin laatikossa se on sijoitettu seuraavasti:

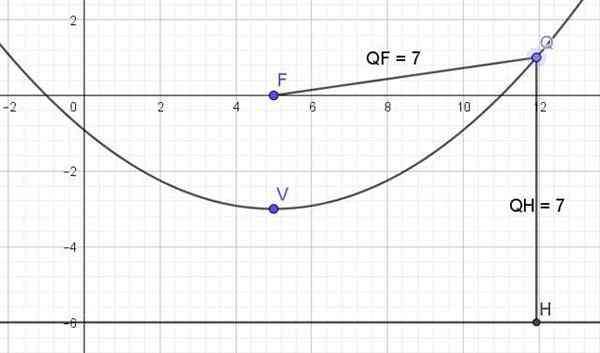Kuva 3. Vertauksen x kaavio² -10x -12y - 11 = 0. Lähde: f. Zapata.

Viitteet

1. Kalju. 1977. Perusalgebra. Venezuelan kulttuuriversiot.
2. Hoffman, J. Matematiikan aiheiden valinta. Nide 2.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
5. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.