Tuhoava häiriökaava ja yhtälöt, esimerkit, liikunta

Se tuhoisa häiriö, Fysiikassa se tapahtuu, kun kaksi riippumatonta aaltoa, jotka yhdistyvät samalla avaruusalueella, ovat vanhentuneita. Sitten yhden aallon harjanteet kohtaavat toisen laaksot ja tulos on aalto, jolla on nolla amplitudi.

Useat aallot kulkevat ilman ongelmia saman avaruuspisteen läpi ja sitten jokainen seuraa polkua ilman, että se vaikuttaa, kuten seuraavan kuvan vedessä olevat aallot:

Kuvio 1. Sadepisarat tuottavat aaltoja veden pinnalla. Kun tuloksena olevilla aaltoilla on nolla leveyttä, sanotaan, että häiriöt ovat tuhoisia. Lähde: Pixabay.

Oletetaan, että kaksi aaltoa, joilla on yhtä suuri amplitudi ja taajuus ω, jota kutsumme ja₁ ja ja₂, Se voidaan kuvata matemaattisesti yhtälöiden avulla:

ja₁= AEN (kx -ω)

ja₂ = SEN (kx -ωt + φ)

Toinen aalto ja₂ Sillä on aukko φ suhteessa ensimmäiseen. Yhdistettynä, koska aallot voidaan päällekkäin ilman ongelmia, ne aiheuttavat tuloksena olevan aallon, jota kutsutaan ja_{R -}-

ja_{R -} = y₁ + ja₂ = SEN (kx -ω) + a sin (kx -ωt + φ)

Trigonometrisen identiteetin kautta:

sin α + sin β = 2 sin (α + β)/2 . cos (α - β)/2

Yhtälö ja_{R -} Se muuttuu:

ja_{R -} = [2a cos (φ/2)] sin (kx - ωt + φ/2)

Nyt tällä uudella aaltolla on tuloksena oleva amplitudi_{R -} = 2a cos (φ/2), joka riippuu vaiheerosta. Kun tämä vaiheero saa arvot+π tai -π, tuloksena oleva amplitudi on:

-Lla_{R -} = 2a cos (± π/2) = 0

Koska cos (± π/2) = 0. Juuri silloin tapahtuu tuhoavia häiriöitä aaltojen välillä. Yleensä, jos kosinin argumentti on muodoltaan ± kπ/2 parittomalla k, amplitudi_{R -}  Se on 0.

[TOC]

Tuhoavia häiriöesimerkkejä

Kuten olemme nähneet, kun kaksi tai useampia aaltoja kulkee samanaikaisesti pisteen läpi, ne ovat päällekkäisiä, aiheuttaen tuloksena olevaan aaltoon, jonka amplitudi riippuu osallistujien välisestä vaiheerosta.

Voi palvella sinua: lineaarinen variaatio: käsite, esimerkit, liikunta ratkaistu

Tuloksena olevalla aaltolla on sama taajuus ja aallonumero kuin alkuperäisillä aaltoilla. Seuraavassa animaatiossa kaksi aaltoa on päällekkäin sinisissä ja vihreissä väreissä. Tuloksena oleva aalto on punaisella.

Amplitudi kasvaa, kun häiriöt ovat rakentavia, mutta se peruutetaan, kun se on tuhoisa.

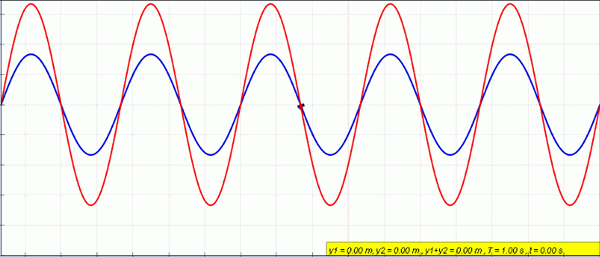Kuva 2. Siniset ja vihreät aallot ovat päällekkäisiä punaisten aaltojen aiheuttamiseksi. Lähde: Wikimedia Commons.

Aaltoja, joilla on sama amplitudi ja taajuus, kutsutaan johdonmukaiset aallot, Niin kauan kuin ne pitävät heidän välilläan saman vaiheen ero φ. Yhtenäinen aaltoesimerkki on laservalo.

Tuhoavan häiriön ehto

Kun siniset ja vihreät aallot ovat vanhentuneita 180 º tietyssä pisteessä (katso kuva 2), se tarkoittaa, että ne liikkuvat, heillä on vaiheerot φ π -radianien, 3π radiaanien, 5π radiaanien ja niin edelleen.

Tällä tavoin jakamalla tuloksena olevan amplitudin argumentti 2: lla se johtaa (π/2) radiaanit (3π/2) radiaanit ... ja tällaisten kulmien kosini on aina 0. Siksi häiriöt ovat tuhoisia ja amplitudi tehdään 0.

Tuhoavat aaltohäiriöt vedessä

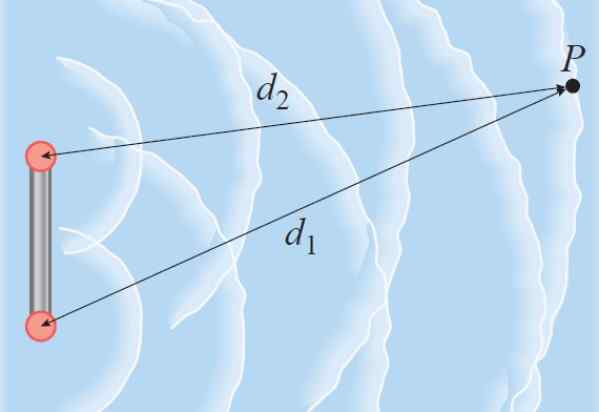
Oletetaan, että kaksi johdonmukaista aaltoa alkavat toisessa. Tällaiset aallot voivat olla ne, jotka leviävät veden läpi kahden värähtelyn ansiosta. Jos nämä kaksi aaltoa kulkevat samaan pisteeseen P, kiertäen eri etäisyyksiä, vaiheero on verrannollinen polkueroon.

Kuva 3. Kahden lähteen tuottamat aallot kulkevat vedessä pisteeseen P. Lähde: Giambattista, a. Fysiikka.

Koska aallonpituus λ on yhtä suuri kuin 2π -radiaanien ero, on totta, että:

│D₁ - d -d₂│ / λ = Vaiheero / 2π radiaanit

Vaiheero = 2π x│d₁ - d -d₂│/ λ

Voi palvella sinua: Valon polarisaatio: Tyypit, esimerkit, sovellukset

Jos teiden polku on pariton määrä aallon puoliaaltoa, toisin sanoen: λ/2, 3λ/2, 5λ/2 ja niin edelleen, niin häiriöt ovat tuhoisia.

Mutta jos tieero on aallonpituuksien vääntömomentti, häiriö on rakentavaa ja amplitudit lisätään pisteeseen P.

Valoaaltojen tuhoisat häiriöt

Kevyet aallot voivat myös häiritä toisiaan, kuten Thomas Young on todennut vuonna 1801 heidän juhlitun kaksoiskokeen kautta.

Young antoi valoa läpinäkymättömällä näytöllä tehdyn raon, joka Huygensin periaatteen mukaan puolestaan ​​tuottaa kaksi toissijaista valolähdettä. Nämä lähteet jatkuivat matkalla toisen läpinäkymättömän näytön läpi, jossa oli kaksi rakoa ja tuloksena oleva valo projisoitiin seinälle.

Kaavio havaitaan seuraavassa kuvassa:

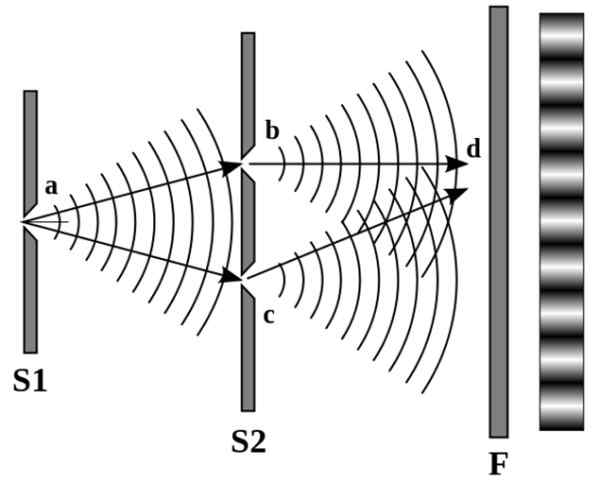Kuva 4. Oikean seinämän valon ja tummien viivojen malli johtuu vastaavasti rakentavista ja tuhoisista häiriöistä. Lähde: Wikimedia Commons.

Young havaitsi erottuvan vaihtoehtoisen valon ja tumman viivan kuvion. Kun valonlähteet häiritsevät tuhoavasti, linjat ovat tummat, mutta jos ne tekevät rakentavasti, linjat ovat selkeät.

Toinen mielenkiintoinen häiriöesimerkki on saippuakuplat. Nämä ovat erittäin ohuita kalvoja, joissa häiriöt tapahtuvat, koska valo heijastuu ja taitetaan pinnoille, jotka rajoittavat saippuakalvoa, sekä ylä- että alapuolella.

Kuva 5. Ohut saippuaelokuvassa muodostuu häiriökuvio. Lähde: PxFuel.

Kuten kalvon paksu. Tuloksena on värikuvio, jos tuleva valo on valkoinen.

Se johtuu siitä, että valkoinen valo ei ole yksiväristä, mutta se sisältää näkyvän spektrin kaikki aallonpituudet (taajuudet). Ja jokainen aallonpituus näyttää eri väriltä.

Se voi palvella sinua: valoisat elimet: ominaisuudet ja kuinka ne tuottavat oman valonsa

Liikuntaa

Kaksi saman oskillaattorin käyttämää identtistä kaiutinta on erotettu 3 metriä ja yksi kuuntelija on 6 metrin päässä kaiuttimien välisestä erotuspisteestä, pisteessä tai.

Siirry sitten pisteeseen P, kohtisuorassa etäisyydellä 0.350 pisteestä tai, kuten kuvassa esitetään. Lopeta äänen kuuntelu ensimmäistä kertaa. Mikä on aallonpituus, jolla oskillaattori säteilee?

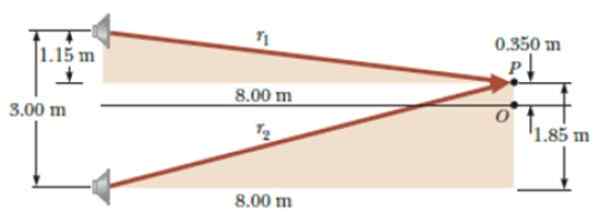Kuva 6. Kaavio harjoitukselle ratkaistu. Lähde: Serway, R. Fysiikka tieteen ja tekniikan fysiikka.

Ratkaisu

Tuloksena olevan aallon amplitudi on 0, siksi häiriöt ovat tuhoisia. Sinun täytyy:

Vaiheero = 2π x│r₁ - r -₂│/ λ

Pythagoras -lause, jota käytetään kuvan varjostettuihin kolmioihin:

r -₁ = √1.viisitoista² + 8² M = 8.08 m; r -₂ = √1.85² + 8² M = 8.21 m

│R₁ - r -₂│ = │8.08- 8.21 │ M = 0.13 m

Pienimmät esiintyvät λ/2, 3λ/2, 5λ/2 ... ensimmäinen vastaa λ/2: ta, sitten faasieron kaavan kanssa on:

λ = 2π x│r₁ - r -₂│/ vaihe -ero

Mutta aaltojen välisen vaiheen on oltava π, niin että amplitudi_{R -} = 2A cos (φ/2) olla nolla, sitten:

λ = 2π x│r₁ - r -₂│/ π = 2 x 0.13 m = 0.26 m

Viitteet

1. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 7. Aallot ja kvanttifysiikka. Toimittanut Douglas Figueroa (USB).
2. Fiscalab. Aaltohäiriö. Toipunut: fisikab.com.
3. Giambattista, a. 2010. Fysiikka. Toinen. Ed. McGraw Hill.
4. Serway, R. Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.
5. Wikipedia. Nukkumislevyn häiriöt. Lähde: Se on.Wikipedia.org.