Magneettiset sokkiyksiköt, kaavat, laskelmat, esimerkit

Se magneettinen sokki o Magneettinen vastus on vastustus siitä, että väliaine edustaa magneettisen vuon kulkua: mitä suurempi on kiiltävä, magneettisen vuodon määrittäminen on vaikeampaa. Magneettisessa piirissä kiiltävällä on sama rooli kuin sähkövastuksella sähköpiirissä.

Sähkövirran kuljettama kela on hyvin yksinkertainen magneettikuvausesimerkki. Virran ansiosta syntyy magneettinen flux, joka riippuu kelan geometrisestä asennuksesta ja myös sen ylittävästä virran voimakkuudesta.

Kuvio 1. Magneettinen muutos on ominaisuus magneettisille piireille, kuten muuntajalle. Lähde: Pixabay.

[TOC]

Kaavat ja yksiköt

Merkitsee magneettista vuotoa Φ_m, Sinulla on:

Φ_m = N.I / (ℓ_c / μA_c-A

Missä:

-N on kelan käännösten lukumäärä.

-Virran voimakkuus on Yllyttää.

-ℓ_c edustaa piirin pituutta.

--Lla_c Se on poikkileikkausalue.

-μ on ympäristön läpäisevyys.

Geometrian ja ympäristön vaikutuksen yhdistävä nimittäjän tekijä on tarkalleen piirin magneettinen isku, skalaarinen määrä, johon se merkitään kirjaimella ℜ, sen erottamiseksi sähkövastuskestävyydestä. Niin:

ℜ = ℓ_c / μ.-Lla_c

Kansainvälisessä yksikköjärjestelmässä (SI) se mitataan ℜ Henrion käänteiseksi (kerrottuna käännösten lukumäärällä n). Henrio puolestaan ​​on magneettisen induktanssin yksikkö, joka vastaa 1 Tesla (t) x neliömetri /ampeerio. Siksi:

1 TUNTI^-1 = 1 A /T.m²

 1 t.m² = 1 Weber (WB), kiiltävä ilmaistaan ​​myös A/WB: ssä (Amperio/Weber.

Kuinka magneettinen sokki lasketaan?

Koska magneettisella iskulla on sama sähkövastuksen rooli magneettisessa piirissä, on mahdollista pidentää analogiaa vastaavalla ohm v = go näille piireille.

Voi palvella sinua: Manometrinen paine: Selitys, kaavat, yhtälöt, esimerkit

Vaikka se ei kiertä kunnolla, magneettinen flux φ_m vaihdetaan virran tila, kun taas jännitteen sijasta V, Se Magneettinen jännitys jompikumpi Magnetomoottorivoima, analoginen sähkömoottori tai F.ja.m Sähköpiireissä.

Magnetomoottorivoima on vastuussa magneettikuon ylläpidosta. Se on lyhennetty F.m.m Ja se on merkitty ℱ. Sen kanssa sinulla on vihdoin yhtälö, joka liittyy kolmeen suuruuteen:

ℱ = φ_m . ℜ

Ja verrattuna yhtälöön Φ_m = N.I / (ℓ_c / μA_c-A, on päätelty-

ℱ = n.Yllyttää

Tällä tavoin kiiltävä voidaan laskea piirin geometrian ja ympäristön läpäisevyyden tuntemisen tai magneettisen vuodon ja magneettisen jännityksen tuntemisen tämän viimeisen yhtälön ansiosta, nimeltään Hopkinsonin laki.

Ero sähkövastuksella

MRI: n yhtälö ℜ = ℓ_c / μA_c Se on samanlainen kuin  R = l / σa Sähkövastuksen suhteen. Jälkimmäisessä σ edustaa materiaalin johtavuutta, L on lankaan pituus ja A on sen poikkileikkauksen pinta -ala.

Nämä kolme suuruutta: σ, l ja a ovat vakioita. Ympäristön läpäisevyys kuitenkin μ, Yleensä se ei ole vakio, niin että piirin magneettinen isku ei ole, toisin kuin sen sähköinen samanlainen.

Jos väliaineesta tapahtuu muutos, esimerkiksi siirtyessäsi ilmasta rautaan tai päinvastoin, läpäisevyys muuttuu, seurauksena kiiltävä vaihtelu. Ja myös magneettiset materiaalit käyvät läpi Hystereesisyklit.

Tämä tarkoittaa, että ulkoisen kentän levitys saa materiaalin säilyttämään osan magnetismista, jopa kentän jälkeen.

Siksi magneettinen sokki lasketaan joka kerta, kun on tarpeen määrittää huolellisesti, missä syklin vaiheessa materiaali on, ja siten sen magnetointi.

Voi palvella sinua: fyysinen optiikka: historia, usein termit, lait, sovellukset

Esimerkit

Vaikka kiiltävä riippuu paljon piirin geometriasta, se riippuu myös väliaineen läpäisevyydestä. Mitä suurempi tämän arvo, sitä alhaisempi on kiiltävä; Näin on ferromagneettiset materiaalit. ILMA: lla on alhainen läpäisevyys, joten sen magneettinen isku on suurempi.

Solenoidit

Solenoidi on hullu pituus ℓ Valmistettu n kierroksella, joiden läpi sähkövirta ohitetaan ja. Käännökset ovat yleensä pyöreitä pyöreästi.

Intensiivisen ja tasaisen magneettikentän sisällä syntyy, kun taas kenttä on valmistettu noin nolla.

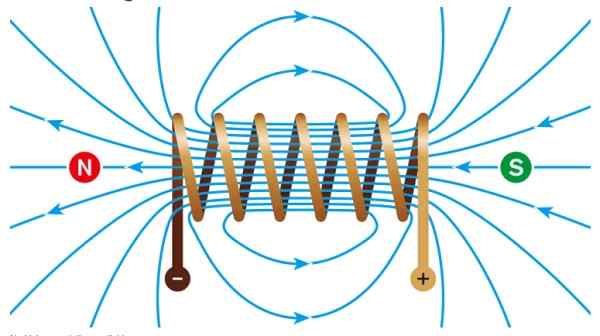Kuva 2. Magneettikenttä solenoidin sisällä. Lähde: Wikimedia Commons. Rajiv1840478 [cc by-s (https: // creativecommons.Org/lisenssit/by-SA/4.0)].

Jos pyöreälle muodolle annetaan pyöreä muoto, on a Toroidi. Sisällä voi olla ilmaa, mutta jos rautaydin asetetaan, magneettinen vuoto on paljon suurempi tämän mineraalin korkean läpäisevyyden ansiosta.

Rullattu kela suorakaiteen muotoisella rautaydin

Magneettinen piiri voidaan rakentaa käärimällä kela suorakaiteen muotoiseen raudan ytimeen. Tällä tavoin, kun virta johdetaan langan läpi, on mahdollista muodostaa voimakas kenttävirta, joka on rajoitettu raudan ytimen sisään, kuten kuvassa 3 voidaan nähdä.

Shilling riippuu piirin pituudesta ja kuvassa ilmoitetusta poikkileikkauksesta. Esitetty piiri on homogeeninen, koska ydin on yhtä materiaalia ja poikkileikkaus pysyy tasaisena.

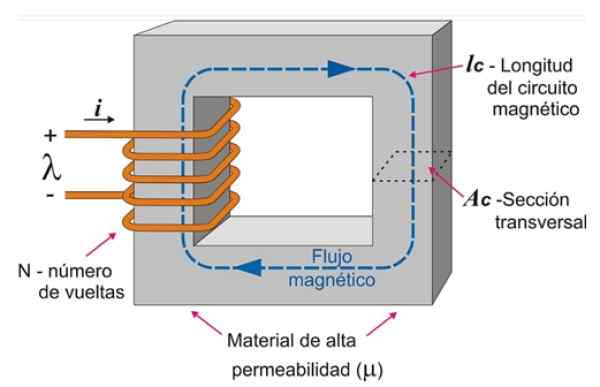Kuva 3. Yksinkertainen magneettinen piiri, joka koostuu kelasta, joka on täynnä rautaydin suorakaiteen muotoista. Vasemman kuvan lähde: Wikimedia Commons. Usein [CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/3.0)]

Ratkaisut

- Harjoitus 1

Löydä vuoden 2000 spiraalirektilinarisen solenoidin magneettinen sokki tietäen, että kiertämällä virta 5 A magneettinen vuoto, 8 mWB, syntyy.

Voi palvella sinua: Sähkömagneettiset aallot: Maxwell -teoria, tyypit, ominaisuudet

Ratkaisu

Yhtälöä käytetään ℱ = n.Yllyttää Magneettisen jännityksen laskemiseksi, koska virran voimakkuus ja kelan käännösten lukumäärä on saatavana. Se yksinkertaisesti moninkertaistaa:

ℱ = 2000 x 5 a = 10.000 amps-vuelta

Sitten ℱ = φ_m . ℜ, Weberin magneettisen vuodon ilmaiseminen (etuliite "m" tarkoittaa "Mili", joten se kerrotaan 10 ^-3-

Φ_m = 8 x 10 ^-3 WB

Nyt shokki puhdistetaan ja arvot korvataan:

ℜ = ℱ/ φ_m = 10.000 amps-vuelta /8 x 10 ^-3 WB = 1.25 x 10⁶ AMPERIO-VUELTA/WB

- Harjoitus 2

Laske kuviossa esitetyn piirin magneettinen isku esitetyillä mittoilla, jotka ovat senttimetrejä. Ytimen läpäisevyys on μ = 0.005655 t · m/a ja poikkileikkaus on vakio, 25 cm².

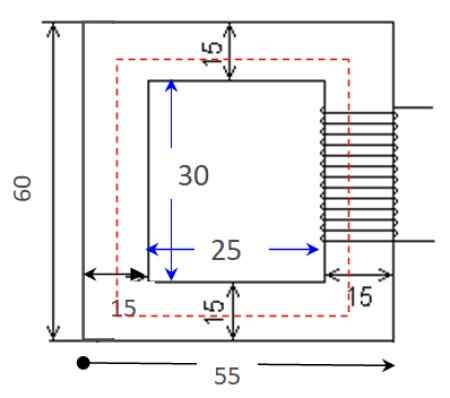Kuva 4. Esimerkin 2 magneettinen piiri. Lähde: f. Zapata.

Ratkaisu

Käytämme kaavaa:

ℜ = ℓ_c / μA_c

Läpäisevyys ja ristikkäinen alue on saatavana tietoina lauseessa. Meidän on löydettävä piirin pituus, joka on kuvan punaisen suorakulmion kehä.

Tätä varten vaakapuolen pituus on keskiarvo, lisäämällä suurempi pituus ja pienempi pituus: (55 +25 cm)/2 = 40 cm. Jatka sitten samalla tavalla pystysuuntaisella puolella: (60 +30 cm)/2 = 45 cm.

Lopuksi lisätään neljän sivun keskimääräiset pituudet:

ℓ_c = 2 x 40 cm + 2 x 45 cm = 170 cm

Lomakannan arvojen korvaaminen on vielä korvata, mutta ei ennen ilmaisua poikkileikkauksen pituuden ja pinta -alan - lausunnossa - yksiköissä, jos:

ℜ = 170 x 10 ^-2m / (0.005655 t · m/a x 0.0025 m²) = 120.248 AMPERIO -VUELTA/WB

Viitteet

1. Saksa, m. Ferromagneettinen ydin. Palautettu: YouTube.com.
2. Magneettinen piiri ja vastahakoisuus. Toipunut: MSE.Ndhu.Edu.Tw.
3. Spinadel, e. 1982. Sähkö- ja magneettiset piirit. Uusi kirjakauppa.
4. Wikipedia. Magnetomoottorivoima. Palautettu: on.Wikipedia.org.
5. Wikipedia. Magneettinen sokki. Palautettu: on.Wikipedia.org.